【正負の数のひき算(減法)】すべてのひき算は、たし算とみなせる？２つの要点を「すごろくのイメージ」でわかりやすく解説！【中１数学・正負の数③】
リチャード
リチャードの大学
「数学で文字式をつかう理由やメリット」を、具体例を交えてわかりやすく解説！【中１数学・文字と式①】
リチャード
この記事は、
- なんで、数学なのに、ｘとかｙとか「文字」なんて使うの？
- 文字式なんて使って、なんかの役に立つの？
という方のために、
数学で、「ｘやｙ」などの文字式をつかう理由とメリット
について、わかりやすく解説していきます！
この記事を読むことで、「なぜ、勉強する必要があるのか」を理解できるため、
- これからの勉強のモチベーションがあがる
- これからの学習の理解度が高まる
といったメリットを得られます！
でも、「負の数」とかっていう、よくわからないものの勉強がやっと終わったかと思いきや、
今度は、ｘやらｙやらを使う「文字式」というものがいきなり出てきて、正直つらいです、、
あと、ｘやｙとかの文字も、ふだんあんまり見ない英語なので、なんだかとっつきづらいんですよね、、
そうですよね、いきなり数学で「文字をつかう！」といわれても、
理由もよく分からないし、戸惑いますよね、、
ですが、ｘやｙなどの「文字式」は、みなさんを困らせるためのものではなく、
実は、これから先に出てくる複雑な問題を解決しやすくするために生み出されたものです！
つまり、
「文字式」は、みなさんが楽をするために生みだされた味方
といえます！
あ、そうだったんですね！
そう聞いて、なんだか「文字式」に親しみを感じてきました！
でも、なぜ、「文字式」が、僕たちの味方になるんでしょうか？
それについては、この記事の中で、
具体例を交えながら、詳しく解説していきます！
この記事を読み終えれば、
「文字式は、なぜ私たちの味方となるのか」
という疑問が、すんなりと理解できるはずです！
それでは、はじめていきましょう！
なぜ、文字式をつかうの？
さっそくですが、結論からいうと、
文字式をつかう理由は、
解決したい問題をシンプルにして、考えやすくするため
です！
つまり、ｘやｙなどの文字式は、一見難しそうですが、
実は「身の回りで出会う、なにかしらの問題」を解決するための味方ともいえます！
そういわれても、まだボヤっとしていて、よく分からないです、、
そうですよね、、
そこで、次から具体的な「問題」をみていきましょう！
問題｜ゲームはいつ買える？
問題
リチャードさんは、おこづかいを毎月1000円もらっており、
現在の所持金は、1500円です。
あるとき、新発売のゲームソフトが欲しくなりました。
ゲームソフトの値段は、5500円です。
来月から、もらえるお金を全部貯金するとしたら、
ゲームソフトを買えるのは、何か月後になるでしょうか？
どうでしょうか？
もしかしたら、すぐに答えを出せた人もいるかもしれませんが、
ここでは、この「問題」に対する２つの考え方をご紹介します！
【考え方１】文字を使わない方法
考え方１
まず、所持金は1500円で、ゲームソフトの値段5500円なので、
貯める必要のあるお金は、5500円-1500円=4000円であることがわかります。
次に、毎月1000円ずつおこづかいをもらえるので、
4000円貯めるのに必要な月数は、\( 4000\div1000=4 \)ヶ月だとわかります。
この考え方が、一般的ですし、もっとも簡単だと思います！
僕も、この考え方で解きました！
ただ、実は、
この問題に対して、もう１つ別の重要な考え方があります！
それを次で、ご紹介します！
【考え方２】文字を使う方法
考え方２
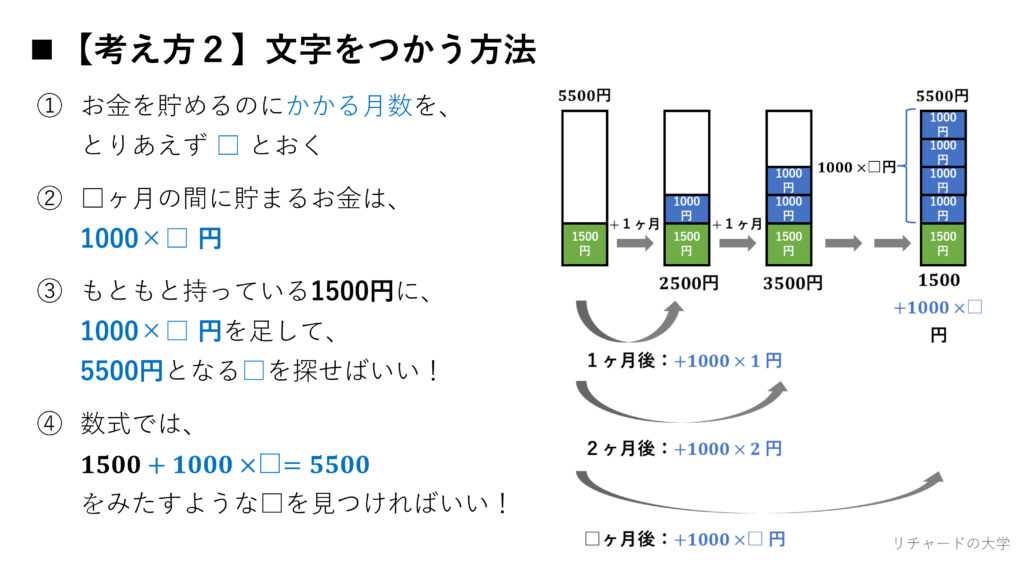
まず、お金を貯めるのにかかる月数は、すぐにはわからないので、
とりあえず、□ と置いてしまいます。
そうすると、毎月1000円のおかづかいをもらえるため、
□ヶ月の期間に、もらえるお金の合計は、1000×□円となります。
よって、もともと持っている1500円に、1000×□円を足して、
ゲームの値段である5500円となるような□をみつければよいことがわかります。
これは、数式をつかうと、
\( 1500+1000\times□=5500 \)
とも表せます。
つまり、この数式を満たすような□をみつければ、それが答えです。
以上が、２つ目の考え方ですが、どうでしょうか？
「考え方１」の方が、短いし、簡単な気がします、、
そうですよね、私も同意見です。
ただ、なぜ、わざわざ「考え方２」を紹介したかというと、
ある重要なポイントを説明したかったからです！
その、「考え方２」の重要なポイントとは、
「わからないもの」を、とりあえず□とおくことで、
解決すべき問題を、
\( 1500+1000\times□=5500 \)
というふうに、数式を使ったシンプルな形にできた
ということです！
今回の問題は単純なため、
「考え方１」を使って、簡単に計算できましたが、
現実に起こる問題や、これから先(高校、大学)で出会う問題は、
複雑な場合が多いです！
そのため、「考え方２」のように、
分からないものを□とおいて、
解決すべき問題を数式というかたちで整理することは、
今後必須となります！
今後必須となるその考え方を伝えるため、
あえてまどろっこしい説明をしたわけです！
ポイント
複雑な問題を考えるときは、
「分からないもの」を、とりあえず「文字(□)」として置くことで、
考えるべき問題を、シンプルな形に整理できる！
数学でわざわざ文字を使う理由が、なんとなくわかってきました！
ただ、数学で、「ｘやｙ」といった文字はよく見るんですが、
「□」なんて文字は、見たことない気がします、、
「ｘやｙ」と「□」は、同じものなんでしょうか？
結論からいってしまうと、同じものです！
今回は「わからないモノ」として、とりあえず「□」という文字を使いましたが、
普通、数学では、「□」ではなく、「ｘやｙ」などの文字を使います！
ただ、「わからないモノを表す」という意味では、
数学で出てくるｘやｙなどの文字は、
けっきょくは、今回使った「□」と本質的に同じものといえます！
話をまとめると、
数学で出てくる「ｘやｙ」などの文字は、今回使った「□」と同じもの
であり、そういった文字をつかう理由は、
「分からないモノ」を、とりあえず文字(□、ｘ、ｙなど)として置くことで、
解決すべき複雑な問題を、
数式を使ったシンプルな形にして、考えやすくしたいから
ということになります！
要するに、数学で出てくる「ｘやｙ」などの難しそうな文字は、
実は、複雑な問題を整理するために生まれた、私たちの味方ともいえます！
なるほど、、「考え方２(文字をつかう考え方)」を使うことで、
\( 1500+1000\times□=5500 \)というふうに、
数式を使ったシンプルな形にできることは理解できました！
ただ、この数式から、「問題の答え」を求めるにはどうしたらいいんでしょうか？
やはり、気になりますよね、、
それでは、これから、答えの求め方を解説していきます！
ただ、「考え方２(文字を使った考え方)で、答えを得る方法」は、
これから先で勉強する「方程式」という分野でも詳しく説明するため、今は分からなくても大丈夫です！
気になる方だけご覧ください！
【参考】考え方２のつづき｜文字を使う方法
考え方２のつづき
お金が貯まるまでにかかる月数を、□と置くことで、
解決すべき問題を
\( 1500+1000\times□=5500 \)
という数式であらわせました。
つまり、この数式を満たすような□をみつければ、それが答えです。
では、□がなにかを考えていきましょう。
まず、\( 1000\times□ \)を１つのかたまりとして、〇と置いてみます。
そうすると、数式は、\( 1500+〇=5500 \)、
つまり、1500＋〇が5500となるような〇をみつければよいことがわかります。
よって、〇=4000だと考えられます。
次に、\( 〇=1000\times□ \)と置いていたことを思い出すと、
4000=1000×□となるような□を見つければよいことがわかります。
□が4であれば、1000×□は4000になるため、答えは4となります。
まとめ
この記事では、
数学で、「ｘやｙ」などの文字式をつかう理由とメリット
について解説しました！
結論として、文字式をつかう理由は、
解決したい問題をシンプルにして、考えやすくするため
でしたね。
今回あつかった問題は、簡単なものだったため、
「文字式をつかうメリット」はあまり分かりませんでしたが、
これから先は、複雑な問題がたくさん出てきます！
そういう複雑な問題を考えるときに、初めて、
「文字式の便利さ」が分かってくるはずです！
なるほど、、
学校では、「文字式の扱い方」については詳しく習いましたが、
「なぜ、文字式をつかう必要があるのか」
については、あまり教えてもらえなかった気がするので、
今回のお話は、とても勉強になりました！
そうですよね、、私もあまり教えてもらえなかった気がします。
ただ、今回お話した、
「文字式をつかうメリットや、モチベーション」を頭にいれておくだけで、
これから先で学ぶ「文字式の扱い方」も、理解しやすくなるはずです！
最後までお読みいただきありがとうございます。
この記事がどなたかの参考になれば幸いです。
次回は、「文字式の表し方のルール」について解説します！
今回のように、「なぜ、ルールがあるのか」というところから
丁寧にわかりやすく説明していきますので、ぜひご覧ください！
次回の記事
最低限知っておくべき「文字式の表し方のルール」と「なぜ、ルールがあるのか」を、具体例を使ってわかりやすく解説！【中１数学・文字と式②】
参考文献
この記事を書くにあたっては、以下の書籍も参考にしています。
created by Rinker
¥1,650
(2024/02/15 02:04:48時点 楽天市場調べ-詳細)
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい！」
という学生や社会人の方に、非常におすすめです！
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という意味では、本ブログに分があると思うので、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです！
その理由は、次の通りです！
動画での学習がオススメな理由
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です！
１４日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓
ABOUT ME
中学・高校では数学が苦手でしたが、
科学が好きだったため、
大学の物理学科に入るべく、数学を猛勉強。
その結果、なんとか物理学科に合格し、
そのまま大学院まで進学。
最終学歴は、物理学の修士号です。
数学が苦手だった経験をいかし、
私と同じように数学に苦しんでいる方の役に立てればと思い、
わかりやすさとイメージを重視して、
このブログを書いています。
科学が好きだったため、
大学の物理学科に入るべく、数学を猛勉強。
その結果、なんとか物理学科に合格し、
そのまま大学院まで進学。
最終学歴は、物理学の修士号です。
数学が苦手だった経験をいかし、
私と同じように数学に苦しんでいる方の役に立てればと思い、
わかりやすさとイメージを重視して、
このブログを書いています。
