「正負の数のかけ算(乗法)・わり算(除法)」の２つの計算ルールをわかりやすく解説！【要点のまとめ】【中１数学・正負の数④】
リチャード
リチャードの大学
最低限知っておくべき「文字式の表し方のルール」と「なぜ、ルールがあるのか」を、具体例を使ってわかりやすく解説！【中１数学・文字と式②】
リチャード
この記事では、
- 「文字式の表し方」のルールと、具体例が知りたい！
- なぜ、「文字式の表し方」には、「ルール」があるの？
という方のために、
- 最低限しっておくべき「文字式の表し方」のルールと具体例
- なぜ、「文字式の表し方」には「ルール」があるのか
について、解説していきます！
「文字式の表し方のルール」ですか、、
「ｘやｙ」などの、あまりなじみのない文字が出てきたなーと思ったら、
「こう書け！」というふうに、いきなり「書き方のルール」を勉強させられて、とまどいます、、
そうですよね、、
理由もわからず、「書き方のルールを勉強しろ」といきなり言われても、とまどいますよね、、
そこで、この記事では、最低限知っておくべきルールはもちろん、
「なぜ、文字式の書き方にルールがあるのか」という、
皆さんが気になることについても解説していきます！
最低限しっておくべき要点に絞って説明するので、
この記事を読むことで、
「文字式の表し方のルール」の本質を、最速で理解できます！
でもそもそも、なぜ「ｘやｙ」などの文字式を使うんでしたっけ？
それについては、前回の記事で、復習しましょう！
あわせて読みたい
「数学で文字式をつかう理由やメリット」を、具体例を交えてわかりやすく解説！【中１数学・文字と式①】
それでは、始めていきましょう！
Contents
最初に知っておくべき
「文字式の表し方のルール」の重要ポイント
さっそく、「文字式の表し方」のルールをご紹介していきたいのですが、
その前に、ルールをみるうえで、知っておくべき重要なポイントをお話しします！
それは、「文字式の表し方」のルールの裏には、
なるべく記号(×、÷)を省略して、
「かけ算」や「わり算」をシンプルに書きたい！
という、思い(モチベーション)がある点です！
要するに、
「かけ算やわり算を書くときに、なるべく楽をしたい！」という思いから、
「文字式の表し方」のルールが生まれた
ということです！
なるほど、、
でも、そのせいで僕たちは、ルールを覚えなきゃいけないんですね、、
たしかに、覚えるのは大変ですよね、、
でも、一度ルールに慣れてしまえば、
とてもシンプルに、かけ算やわり算を書けるようになります！
つまり、これからご紹介する「ルール」は、皆さんの味方です！
このことを頭にいれたうえで「ルール」をみると、少しはとっつきやすくなるのではないでしょうか。
でも、そもそも、
なぜ、シンプルに、かけ算やわり算を書きたいんでしょうか？
それについては、少し長くなるため、
という節で、解説していきますので、少々お待ちください。
とにかく、まずは、ルールを知り、慣れていくことが重要ですので、
さっそく、次から「文字式の表し方」のルールをご紹介していきます！
「文字式の表し方」のルール
さっそく結論からいうと、「文字式の表し方」のルールは次のように決められています！
「文字式の表し方」のルール
- かけ算の記号(×)は、省略する
例. \( 2 \times x = 2x \) - 「数字」と「文字」のかけ算では、「数字」を前につける
例. \( x \times 2 = 2x \) - 「１」のかけ算は、省略する
例. \( 1 \times x = x \) - 「文字」どうしのかけ算は、アルファベット順にならべる
例. \( y \times x = xy \) - おなじ「文字」どうしのかけ算は、指数をつかって表す
例. \( x \times x = x^2 \) - わり算(÷)は、分数をつかって、かけ算(×)に書き直す
例. \( x \div 2 = x \times \frac{1}{2} = \frac{1}{2} x \)
「指数ってなんだっけ？」という方は、ぜひ以下の記事を参考にしてみてください！
あわせて読みたい
累乗(るいじょう)と指数（しすう）をやさしい言葉で、わかりやすく解説！【イメージ中心】【中１数学・正負の数⑥】
なんだか、たくさんルールがありますね、、
たしかに項目は多いかもしれませんね、、
ただ、どのルールにも、先ほどご説明した、
「なるべく記号(×、÷)を省略して、
「かけ算」や「わり算」をシンプルに書きたい！」
という考えが、根底にあることがわかると思います！
残念ながら、このルールは世界的に決められているため、
皆さんは、このルールを覚える必要があります。
そこでまずは、このルールに慣れるため、基本的な例題をみていきましょう！
「文字式の表し方」の例題
例題
- \( y\times 3 \times x \)
- \( (-1)\times x \times y \times x \)
- \( x\times x \times x \div(x) \) (ただし\( x\)はゼロではない)
【例題１】順番はどうなる？
例題１
\( y\times 3 \times x \)
例題１は、次のように考えることができます！
例題１で重要な点は、
「数字と文字の順番を、ルールどおりに並べられるか」
ということだけです！
文字と数字では、数字を先頭にもっていき、
文字どうしでは、アルファベット順に並べればいいんですね！
また、かけ算を省略することで、
たしかに数式がスッキリしましたね！
おっしゃる通り、
「文字式の表し方のルール」を守れば、
かけ算をシンプルな形にまとめられることがわかると思います！
【例題２】(-1)と累乗の扱いはどうなる？
例題２
\( (-1)\times x \times y \times x \)
例題２は、次のように考えることができます！
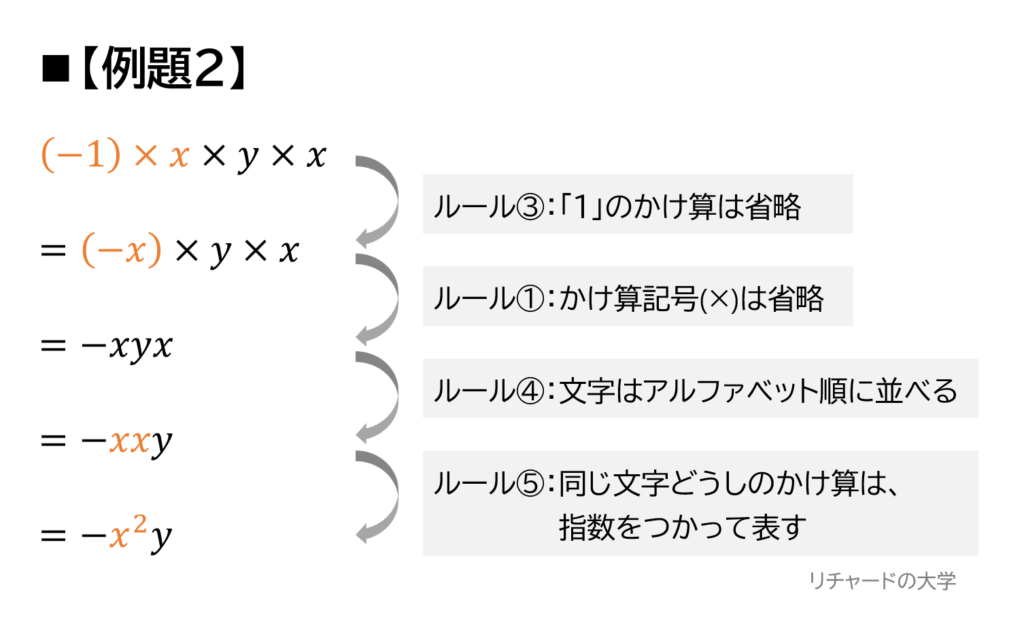
例題２は、「(-1)のかけ算や、指数をどう扱うか」という問題です！
(-1)のかけ算に関しては、「負の数のかけ算」の記事で学んだように、
(マイナス)×(プラス)のかけ算の符号は、(マイナス)になる
ことと、今回のルールにある
「１」のかけ算は省略できる
ことを使えば、(-x)という形にまとめることができます！
ここで、重要な点は、
(-1)をかけ算すると、
「かけられたもの」の符号がひっくり返っていること
です！
あ、ほんとうですね！
ｘの符号は、もともとプラスだったのに、
(-1)をかけ算したら、(-x)となって、正反対の符号になっています！
なぜ、こんなことが起きるんでしょうか？
理由としては、「負の数のかけ算」の記事で学習したように、
マイナスの数にマイナスをかけるとプラスになる一方、
プラスの数にマイナスをかけるとマイナスになるからです！
さらに「１」という数字は省略できるため、
あたかも元の符号をひっくり返したようにみえます！
ポイント
(-1)をかけると、
「かけられたもの」の符号がひっくり返る
次に、指数の取り扱いについては、「累乗と指数」の記事を見ていただければ大丈夫かと思いますが、
累乗があったとしても、アルファベット順に並べるということは注意です！
【例題３】文字式のわり算はどうなる？
例題３
\( (-1)\times x \times y \times x \)
最後に、例題３は次のように考えることができます！
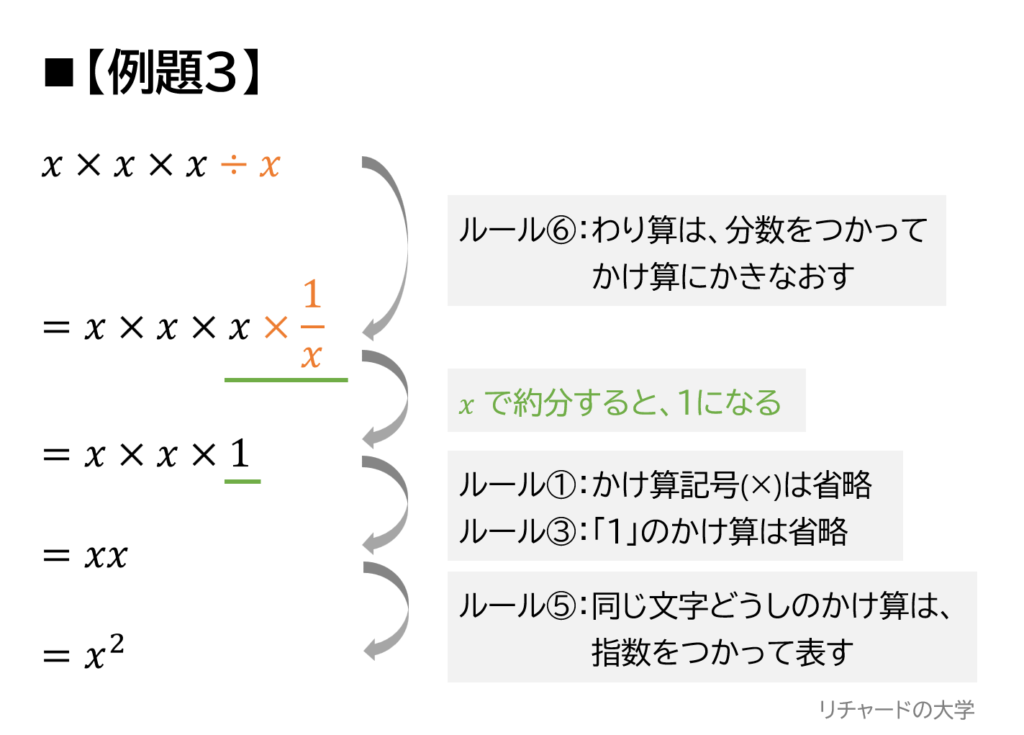
例題３で重要な点は、「文字でわり算したらどうなるのか」という点です！
まずは、文字ではなく、ふつうの「数」のわり算を思い出してみましょう！
ふつうの「数」のわり算の場合、かけ算に書き直すにはどうすればよかったでしょうか？
「わる数」の「分子」と「分母」を入れ替えた分数を使えば、
わり算をかけ算に書き直せます！
そのとおりです！
例えば、÷２は、×1/2 に書き直せるんでしたね。
実は、「文字」でわる場合も、まったく同じです！
例えば、÷ｘは、×1/x に書き直すことができます！
ポイント
「文字」でわり算する場合、「数字」でわり算するときと同様に、
「わる数」の「分子」と「分母」を入れ替えた分数(逆数)を使えば、
わり算をかけ算に書き直すことができる！
ただ注意として、文字でわる場合は、文字がゼロでないかのチェックが必要です。
なぜなら、数学では、
「ゼロでわること、例えば1/0というのは、NG」という決まりがあるからです。
このことは、これから先、文字式を使っていくうえでとても重要なので、
ぜひ覚えておきましょう！
ポイント
数学では、「ゼロ」でわり算するのは、NG！
では、「文字式の表し方のルール」に慣れてきたところで、
最後に「なぜ、文字式の表し方には、ルールがあるのか」
について解説していきます！
なぜ、「文字式の表し方」にはルールがある？
結論から言ってしまうと、
「文字式の表し方」にルールがあることの、最も深い理由は、
「解決すべき複雑な問題」をなるべくシンプルな形にしたいから
です！
この記事の冒頭で、「文字式の表し方のルール」には、
なるべく記号(×、÷)を省略して、
「かけ算」や「わり算」をシンプルに書きたい！
という考えが、根底にあるとお話ししました！
でも、そもそも、
なぜ、かけ算やわり算をシンプルに書きたいんでしょうか？
つまり、まとめると、
「複雑な問題を解決するために、
その問題を数式のかたちで整理することが必要！」
⇒「数式をさらにシンプルにするために、かけ算やわり算を省略しよう！」
という流れになります！
すみません、まだぼやっとしていて、よくわからないです、、
そうですよね、、
前回の記事の「問題」を使って、具体的にみてみましょう！
具体的にどんな問題だったかは、これからの話には関係ありませんが、
気になる方は、以下の記事をご覧ください！
あわせて読みたい
「数学で文字式をつかう理由やメリット」を、具体例を交えてわかりやすく解説！【中１数学・文字と式①】
具体例をとおして、理解しよう！
前回の記事の「問題」では、
以下の数式をみたすような□を見つければ、それが答えだという話をしました！
\( 1500+1000\times□=5500 \)
でも、そもそも「数式をみたす」ってどういうことですか？
今回の場合、「数式をみたす」というのは、
イコール(=)の左側と右側の数字がおなじになることをいいます！
イコール(=)というのは、「同じ(等しい)」ことを表す記号なので、
「イコール(=)でつながっている左側と右側が同じでないと困る」
というわけです！
ちなみに、イコール(=)は等号とも呼ばれ、
イコール(=)の左側を左辺、右側を右辺と呼びます！
この言葉は、これから非常によく使うので、覚えておきましょう！
ポイント
「数式をみたす」というのは、
イコール(=)の左側と右側の数字がおなじになることをいう
ここで、「□」と「ｘ」のどちらも、
「分からないものを、とりあえず文字として置いたもの」という意味では同じものなので、
今回の記事の内容に合わせて、「□」を「ｘ」に置き換えておきましょう！
つまり、
\[ 1500+1000\times x=5500 \]
をみたすようなｘを見つければ、それが答えになります！
言い換えると、
イコール(=)の左側(左辺)と右側(右辺)が同じになるような、
ｘに入る数字をみつければOK！
ということです！
では、実際にそのようなｘを見つけてみましょう！
【ｘを見つける方法１】数字を１つずつ入れていく
ｘをみつける１番単純な方法は、
数字を１つずつｘに入れていき、右辺と左辺が同じかチェックする方法
です！
ここで「文字(x)に、数字をいれること」を代入と呼び、
「代入して計算し、得られた数」を式の値といいます！
ポイント
「文字に、数字をいれること」を代入と呼び、
「代入して計算し、得られた数」を式の値という
例えば、\( x=1 \)として、ｘに１を代入してみましょう！
そうすると、左辺は、\( 1500+1000\times 1 =2500 \) (式の値)となります。
一方、右辺は、\( 5500 \)なので、左辺と右辺は同じではないことが分かります。
つまり、\( x=1 \)ではないということです！
このように、「ｘに１つずつ数字をいれて、左辺と右辺をチェックしていけば、
いつか、数式をみたす数字に出会えるのでは？」というのが１つ目の考え方です！
でも、こんなの時間がかかりすぎませんか？
おっしゃる通りです！
普通は、次でご紹介する「一発でｘをみつける方法」を使います！
【ｘを見つける方法２】一発でみつける
この方法では、次のように考えて、ｘをみつけていきます！
詳しく解説すると、次のような順番で考えていきます！
\(1000\times x=A\) とおく
ここで重要なのは、\(1000\times x=A\)とおくことで、
\(1000\times x\)を１つの「かたまり」として考えている点です。
\(A\) にあてはまる数字は、4000しかないことがわかる
\(A=4000\)とすれば、
\(1500 + A=5500\)という数式の左辺と右辺が同じになることがわかります。
\(1000\times x=A\)と置いていたことを思い出す
STEP2で、\(A=4000\)ということが分かったので、
あとは、「\(1000\times x=4000\)という数式をみたすｘを見つければよい」ということが分かります。
\(x\)にあてはまる数字は、４しかないことがわかる
\(x=4\)とすれば、\(1000\times x=4000\)の左辺と右辺が同じになるとわかるため、
答えは４だと求められます。
この考え方で重要な点は、
\(1000\times x\)を「１つのかたまり」として考え、\(A\)と置いた点
です！
こうしたことで、\(1500 + 1000\times x=5500\)というもともとの数式を、
\(1500 + A=5500\)というさらにシンプルで、考えやすい形にすることができました！
その結果、「わからないもの」である\(A\)や\(x\)に何の数字が入ればいいかが
分かりやすくなり、問題を解くことができたというわけです。
たしかに、\(1500 + A=5500\)という数式だったら、
\(A\)に何の数字が入りそうか、簡単にわかりますね！
そうですよね！
このように、問題を解くときには、
かけ算している部分を「１つのかたまり」とみなして、
問題を解きやすいようにシンプルにしていくこと
が重要となります！
ポイント
かけ算している部分を「１つのかたまり」とみなせば、
数式をシンプルにできるため、問題が解きやすくなる！
でも、今回みたいに、
毎回「かたまり」を\(A\)と置くことは、面倒な気がします、、
そうですよね、、
そこで、かけ算記号(×)を省略するなどして、
なるべく、かけ算している部分を「１つのかたまり」のように見せる工夫をします！
それが、この記事でご紹介した「文字式の表し方のルール」というわけです！
以上のことをまとめると、
かけ算している部分を「１つのかたまり」とみなすと、問題が解きやすくなる！
⇒ かけ算記号(×)などを省略して、
「１つのかたまり」として考えられるようにしよう！
という流れになります！
話が長くなってしまいましたが、
「なぜ、文字式の表し方にルールがあるのか」が、なんとなく分かってもらえたら嬉しいです！
まとめ｜最低でも覚えてほしいこと
この記事では、
- 最低限しっておくべき「文字式の表し方」のルールと具体例
- なぜ、「文字式の表し方」にルールがあるのか
について解説しました！
まず、「文字式の表し方のルール」は、次の通りでしたね。
「文字式の表し方」のルール
- かけ算の記号(×)は、省略する
- 「数字」と「文字」のかけ算では、「数字」を前につける
- 「１」のかけ算は、省略する
- 「文字」どうしのかけ算は、アルファベット順にならべる
- おなじ「文字」どうしのかけ算は、指数をつかって表す
- わり算(÷)は、分数をつかって、かけ算(×)に書き直す
残念ながら「文字式の表し方のルール」は、数学における決まりのようなものなので、
とにかく慣れて、覚えていくしかありません！
しかし、一回慣れてしまうと、手放せなくなるくらい便利なものになってきます！
これからもどんどん使っていきますので、ぜひ、たくさん使って覚えていってください！
次に、「文字式の表し方にルールがある理由」は、
記号(×)などを省略し、かけ算部分を「１つのかたまり」とみなすことで
「解決すべき複雑な問題」を、なるべくシンプルな形にしたいから
でしたね。
これは、「文字式の表し方」を学習するときのモチベーションにもなりますので、ぜひ頭にいれておいてください！
また、この「なぜ、文字式の表し方にルールがあるのか」という節で、
「問題を解く(数式をみたすようなｘを求める)」ということをやりましたが、
実は、あの数式は方程式と呼ばれており、
次に学習する「方程式」という分野で、解き方を詳しく勉強していきます！
あれ、でも、今回の「問題」では、もう解けてしましたよね？
おっしゃる通りです！
みなさんは、もうすでに、「方程式」を解いてしまいました！
つまり「方程式」というのは、いっけん難しそうな名前ですが、
中身はそんなに難しくないということです！
ぜひ自信をもって、これから先の分野に進んでいってください！
そういわれると、なんだか自信がついてきました！
最後に質問なのですが、今回は、
数式をシンプルにするために、
かけ算やわり算の部分を、１つのかたまりとしてまとめる
というお話でしたが、
「たし算やひき算をまとめる」ということはできないんでしょうか？
結論から言ってしまうと、「同じ文字をもつ部分」であれば、
たし算やひき算をまとめることができます！
ただ、詳しく説明するためには、
「１次式」や「同類項」といった考え方を知る必要があります！
そこで、次回の記事では、
「１次式」や「同類項のまとめ方」について解説します！
数式だけみると難しいですが、
今回の記事ように、なるべく図解を使って、
直感的に理解できるように説明しますので、ぜひご覧ください！
次回の記事
１次式ってなに？「同類項のまとめ方」や「なぜ、まとめられるのか」についてわかりやすく解説！【中１数学・文字と式③】
参考文献
この記事を書くにあたっては、以下の書籍も参考にしています。
created by Rinker
¥1,650
(2024/02/15 02:04:48時点 楽天市場調べ-詳細)
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい！」
という学生や社会人の方に、非常におすすめです！
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という面では、本ブログに分があると思うため、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです！
その理由は、次の通りです！
動画での学習がオススメな理由
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です！
１４日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓
ABOUT ME
中学・高校では数学が苦手でしたが、
科学が好きだったため、
大学の物理学科に入るべく、数学を猛勉強。
その結果、なんとか物理学科に合格し、
そのまま大学院まで進学。
最終学歴は、物理学の修士号です。
数学が苦手だった経験をいかし、
私と同じように数学に苦しんでいる方の役に立てればと思い、
わかりやすさとイメージを重視して、
このブログを書いています。
科学が好きだったため、
大学の物理学科に入るべく、数学を猛勉強。
その結果、なんとか物理学科に合格し、
そのまま大学院まで進学。
最終学歴は、物理学の修士号です。
数学が苦手だった経験をいかし、
私と同じように数学に苦しんでいる方の役に立てればと思い、
わかりやすさとイメージを重視して、
このブログを書いています。
