【保存版】「正負の数」のまとめ【中1数学・正負の数】

この記事では、
- テストのために、とにかく、「正負の数」の要点を知りたい!
- 「正負の数」を最短で復習したい!
という方のために、
最低限しっておくべき「正負の数」の要点
について、まとめます!
この記事を読むことで、
最低限必要な「正負の数」の知識を得ることができるため、
テスト前など、最短で「正負の数」を勉強したいときに最適な内容となっています!

内容としては、これまでの記事の復習となります!
それぞれの章に、関連する記事のリンクをはっておきますので、
詳しくはリンク先の記事をご覧ください!
それでは、はじめていきましょう!
そもそも、正負の数とは?
「正負の数」とは?
「正負の数」というのは、
「数の世界」をさらに広げるため、新たに決められた「数」の考え方です!
具体的には、次のような3つのルールで決められています!
- 0よりも大きい数を、正の数とよび、
+(プラス)という記号(符号)をつけて表す
(プラス記号は省略できる)
例. +1, +5, +5.5 (1, 5, 5.5) など - 0よりも小さい数を、負の数とよび、
ー(マイナス)という記号(符号)をつけて表す
(マイナス記号は省略できない)
(例. -1, -5, -5.5 など) - 0は、正の数でも負の数でもない数

といっても、これだけではイメージしにくいと思うので、
次に、中学校から使う「数」は、どんなイメージになるのかを、すごろくの例を使って説明していきます!
「正負の数」のイメージ|すごろく
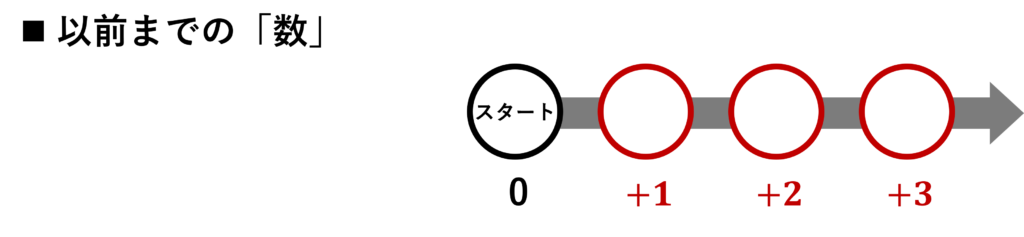
このすごろくでは、小学校までにならった「数」の範囲を表しています。
この図から
小学校までの「数」の範囲を、すごろくで例えると、
スタート(基準点)をゼロとして、
片側の範囲のみ、コマを動かせるすごろく
とみなせる
ということがわかります!
一方、中学校から使う「数」のイメージは、次の図のようになります!
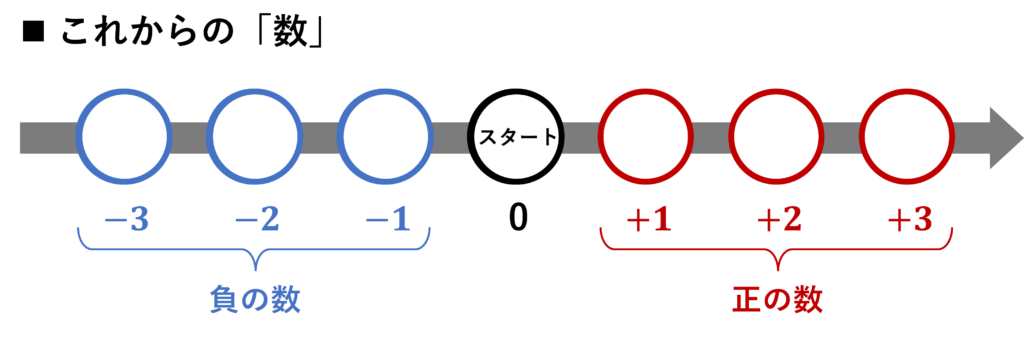
この図から、
負の数を、すごろくでイメージすると、
スタート(ゼロ)に対して、反対側(後ろ側)のコマの位置
とみなせる
ということがわかります!
要するに、
小学校までの「数」に対して、0より小さい「数」(負の数)まで考える
というのが、中学校からの「数」の範囲です!
さらに詳しく知りたい方は、以下の記事や動画を参考にしてみてください!
「負の数」を使うメリット|2つ
筆者の考える「負の数を使うメリット」は次の2つです!
- 「ある基準よりも小さい数」を表せる
- 「正反対のこと」を表せる
1つ目のメリットの例としては、平均点(基準点)があります!
負の数を使うことで、平均点(基準点)よりも下の点数をあらわすことができます!
2つ目のメリットの例としては、先ほどのすごろくの例があげられます!
負の数を使うことで、後ろ方向に進むこと(正反対のこと)をあらわすことができます!
こちらについても、さらに詳しく知りたい方は、以下の記事を参考にしてみてください!

絶対値とは
結論からいうと、
絶対値とは、ゼロ(基準点)から、どれだけ離れているか(ゼロからの距離)
例. +3の絶対値は3、ー3の絶対値は3
のことをいいます!
すごろくの例を使って、イメージすると、次のようになります!

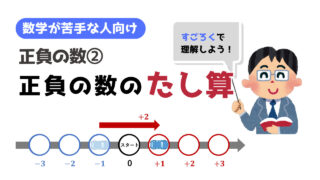
正負の数のたし算(加法)
「正負の数のたし算」のやり方
「正負の数のたし算」は、次の方法で、計算することができます!
- 同じ符号どうしのたし算は、
符号を無視して、たし算をおこない、
最後にもとの符号をつける
例.
\( (+2) + (+1) = +3 \)
\( (-1) + (-2) = -3 \) - 違う符号どうしのたし算は、
それぞれの数の差を計算し、
大きかった数の方の符号をつける
例.
\( (-1) + (+2) = +1 \)
\( (+2) + (-1) = +1 \)
以上の2つのルールを使うことで、
「正負の数のたし算」であれば、どんな問題でも計算することができます!

でも、なぜ、このルールで計算できるのでしょうか?

それについては、以下の記事において、
すごろくのイメージを使って詳しく解説していますので、
ぜひ参考にしてみてください!
また、具体的な例題についても解説しています!
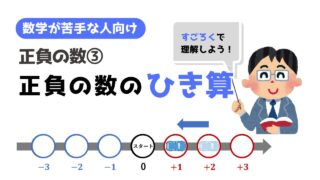
正負の数のひき算(減法)
「正負の数のひき算」の3つの要点
最低限覚えてほしい「正負の数のひき算」の要点は、次の3つです!
- 「正の数を引くこと」は、
「負の数を足すこと」とおなじ
(正の数のひき算は、負の数のたし算とみなせる)
例.
\( (+2) – (+1) = (+2) + (-1) = +1 \) - 「負の数を引くこと」は、
「正の数を足すこと」とおなじ
(負の数にもう1つマイナス符号がつくと、正の数になる)
例.
\( (+2) – (-1) = (+2) +1 = +3 \)
1つ目の要点
まず1つ目については、
「正の数を引く計算」は、小学校でやった「ひき算」と同じ
くらいに理解してもらえれば、簡単に計算できると思います!
2つ目の要点
次に2つ目については、かっこ()の中にも書いてありますが、
負の数にもう1つマイナス符号がつくと、正の数になる
ことを覚えておけば、機械的に計算できます!

すみません、やはり、
「なぜ、そのように計算できるのか」のイメージがつきません、、

そうですよね、、
それについては、以下の記事でくわしく説明していますので、
ぜひ参考にしてみてください!
正負の数のかけ算・わり算
「正負の数のかけ算・わり算」の重要ポイント
「正負の数のかけ算・わり算」において、重要となるポイントは、以下の通りです!
わり算は、逆数をつかうことで、かけ算に書きなおせる
例. \( 2 \div 2 = 2 \times \frac{1}{2} \)
つまり、すべての「わり算」は、「かけ算」に書き換えられるということです!
こうすることで、
「わり算のときは、符号ってどうなるんだっけ?」
ということを悩まずに、
「かけ算の計算ルール」のみを使って、わり算の答えを求めることができます!
それでは次に、「正負のかけ算・わり算の計算ルール」を見ていきましょう!
「正負の数のかけ算(乗法)・わり算(除法)」の2つの計算ルール
「わり算は、逆数をつかうことで、かけ算に書きなおせる」
というポイントを使うことで、
かけ算・わり算の計算ルールは、以下のように、シンプルにまとめることができます!
- わり算は、逆数をつかって、かけ算にかきかえる
- かけ算では、
まず符号を無視して(絶対値どうしで)かけ算をおこない、
その答えに、以下のルールを守って、符号をつける
- (プラス)×(プラス)のときは、プラス符号をつける
例. \( (+1)\times(+2) = +2 \) - (プラス)×(マイナス)のときは、マイナス符号をつける
例. \( (+1)\times(-2) = -2 \) - (マイナス)×(マイナス)のときは、プラス符号をつける
例. \( (-1)\times(-2) = +2 \)
- (プラス)×(プラス)のときは、プラス符号をつける
このルールを使うことで、
「正負の数のかけ算(乗法)・わり算(除法)」は、どんな問題でも計算できます!

すみません、これだけだと、
どう計算すればいいかのイメージがつかないです、、

そうですよね、、
それについては、以下の記事で
交換法則・結合法則
交換法則・結合法則とは?|ひとことで解説!
「交換法則・結合法則とは何か」をひとことでまとめると、次のようになります!
「2つの数のかけ算」では、かける順番を交換してもOK!
例. \( (+1)\times(-2) = (-2)\times(+1) \)
「3つ以上の数のかけ算」では、どこからかけ算をしてもOK!
例.
\( \{(+3) \times (+2)\} \times(+5) \)
\(= (+3) \times \{(+2) \times(+5)\} \)
※\( \{\} \) は、先に計算をおこなう部分をあらわす

なるほど、、
言葉の中身は分かりましたが、
このような法則を考えるメリットって何かあるんでしょうか?

もちろんあります!
交換法則・結合法則のメリットについては、
以下の記事でくわしく解説していますので、ぜひ参考にしてみてください!

また、この交換法則・結合法則をつかうことで、
「3つ以上の数のかけ算」も計算することができます!
「3つ以上の数のかけ算」をどう計算するかについては、次の節で説明します!
「3つ以上の数のかけ算」の計算ルール
「3つ以上の数のかけ算」の計算ルールは、次のようになります!
- まず、符号を無視して、かけ算をおこなう
- つぎに、以下のルールを守って、答えの符号をきめる
- マイナス符号の数が偶数なら、答えの符号はプラス
例. (マイナス)×(プラス)×(マイナス)=(プラス)
\( (-1)\times(+2)\times (-2) = +4 \)
- マイナス符号の数が奇数なら、答えの符号はマイナス
例. (マイナス)×(マイナス)×(マイナス)=(マイナス)
\( (-1)\times(-2)\times (-2) = -4 \)
- マイナス符号の数が偶数なら、答えの符号はプラス

ルールはわかりましたが、
なぜ、答えの符号は、マイナス符号の数で決まるのでしょうか?

その理由は、
「交換法則」と「結合法則」を使うと、かんたんに理解できます!
詳しくは、以下の記事で解説していますので、ぜひご覧ください!

累乗(るいじょう)と指数(しすう)
累乗(るいじょう)や指数(しすう)ってなに?
結論からいうと、
累乗(るいじょう)とは、「同じ数」どうしのかけ算のこと
であり、
指数(しすう)とは、「同じ数」を何回かけているか
を表します!
イメージをつかむため、2の累乗の具体例を考えると、次の図のようになります!


指数や累乗について、なんとなくわかりました!
でも、そもそもなぜ、わざわざこんな書き方をするんでしょうか?

指数をつかって、累乗をかく理由は、
「同じ数」どうしのかけ算を、かんたんに、まとめて書けるから
です!
詳しくは、以下の記事で解説していますので、ぜひ参考にしてみてください!

負の数のとき、累乗や指数はどうなる?
結論からいってしまうと、
負の数のときでも、累乗や指数の意味はおなじ
です!
ただ、正の数のときとは、扱い方が大きく変わってくるので、注意が必要です!
負の数の累乗や指数の考え方で、もっとも重要なポイントは、
指数は、「直前のもの」だけしか、見ることができない
というものです!

まだ、ぼやっとしていて、まだよくわからないです、、

そうですよね、、
そこで、具体的に、次の2つの例題をみていきましょう!
【例題1】「かっこ()がないとき」の負の数の累乗

例題1の場合、指数(2)は、直前のもの(3)しか見えないため、
3だけが2回かけ算されることになります!
【例題2】「かっこ()があるとき」の負の数の累乗

例題2の場合、指数(2)は「直前のもの」であるかっこ()の中身全体をみています。
そのため、(ー3)全体が2回かけ算されることになります!
これらの例題については、以下の記事でもくわしく解説していますので、
ぜひご覧ください!

四則の混じった計算
そもそも、四則(しそく)ってなに?
結論からいうと、
「四則」とは、たし算、ひき算、かけ算、わり算の4つ
のことをいいます!
どれも、この記事で解説してきたものばかりですね。
ただ、この四則が混ざった計算では、計算の優先順位に気を付ける必要があります!
そこで、その計算の優先順位について、次の節で解説していきます!
四則の中で、どれから先に計算すればいい?
結論から言うと、「四則が混じった計算(四則演算)」は、次の順番で計算していきます!
- かっこ()の中
- 累乗(かけ算)
- かけ算・わり算
- たし算・ひき算

すごくシンプルですね!
でもこれだけだと、実際の計算のイメージがつかめないです、、

そうですよね、、
実際の計算例については、以下の記事でくわしく解説していますので、ぜひ参考にしてみてください!

参考文献
この記事を書くにあたっては、以下の書籍も参考にしています。
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい!」
という学生や社会人の方に、非常におすすめです!
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という意味では、本ブログに分があると思うので、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです!
その理由は、次の通りです!
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です!
14日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓