1次式ってなに?「同類項のまとめ方」や「なぜ、まとめられるのか」についてわかりやすく解説!【中1数学・文字と式③】

この記事では、
- 「1次式」ってなんだっけ?
- 「同類項」ってなんだっけ?
- なんで、「同類項」はまとめられるんだっけ?
という方のために、
- 1次式とはなにか
- 「同類項」の具体的なまとめ方
- 「同類項」をまとめられる理由
について、なるべく難しい言葉を使わずに説明していきます!
「具体的な計算方法」だけでなく、「理由」まで丁寧に解説していくため、
この記事を読むことで、
今後の分野にも応用できるような、本質的な理解を得ることができます!

「数式をシンプルにするために、
かけ算やわり算の部分を、1つのかたまりとしてまとめよう!」
というお話をしましたが、
「たし算や引き算は、どうまとめればいいか」
については、説明しませんでしたね。
例えば、以下の数式は、たし算を更ににまとめて、よりシンプルにすることができます!
\[ x+3+2x+1 \]
そこで、この記事では、
「1次式」の場合における「たし算や引き算のまとめ方」について解説していきます!

ちょっと待ってください!
そもそも、「1次式」ってなんですか?


なぜ、他にも種類があるのに、
今回は、「1次式」だけの説明なのでしょうか?

「1次式」というのが、最も基本的な形をしているからです!
1次式で学んだことは、2次式や3次式などでも応用できます!
ちなみに、中学校では、1次式と2次式しか習いません。
そういうわけで、この記事の構成としては、
まずは、重要事項である「1次式とはなにか」について解説し、
その次に「1次式の場合に、たし算やひき算を、どうまとめるのか」について説明していきます!
そして最後に、「なぜ、たし算やひき算をまとめられるのか」についても解説します!

それでは、始めていきましょう!
そもそも、「1次式」とは?
さっそく結論から言ってしまうと、1次式とは、
「文字1個のかけ算のかたまり(項)」までしか含まない数式
です!

すみません、、ぼやっとしていて、まだよく分からないです、、
そもそも、「項」ってなんですか?

「項」というのは、数式の中で、
たし算や引き算で分けられた「ひとかたまり」のことをいいます!
といっても、まだよく分からないと思いますので、
「項」や「1次式」について、それぞれ詳しく見ていきましょう!
項とは?|たし算や引き算で分けられた「ひとかたまり」


まず「項」というのは、先ほどご説明したように、
たし算(+)や引き算(-)で分けられた「ひとかたまり」のことです。
では、\( 2x+1 \)という式の中で、どれが「項」なのでしょうか?

「項」は、たし算(+)で分けられた「ひとかたまり」ですよね、、
\( 2x+1 \)には、\( 2x\)と\( +1 \)の間にだけ、たし算が1つあるので、
\( 2x\)と\( +1 \)が「項」でしょうか?

正解です!
答えは、図にかいてあるように、\( 2x\)と\( +1 \)が項になります!
なぜなら、おっしゃる通り、この数式には、\( 2x\)と\( +1 \)の間にたし算(+)が1つあり、
このたし算によって、\( 2x\)と\( +1 \)が「分けられている」とみなせるからです!
ちなみに、数式の左から1つめの項を第1項、2つ目の項を第2項と呼びます!
さらに、3つ目以降についても、第3項、第4項、、という具合です。
例えば、\( 2x+1 \)の場合、第1項は\( 2x\)、第2項は\( 1 \)となります!
これは意外とこれからよく使っていく言葉なので、できれば覚えておきましょう!
数式において、左から1つめの項を第1項、
左から2つ目の項を第2項と呼ぶ
また、「文字(図の例ではx)にかかっている数」を、係数と呼びます!
例えば、\( 2x\)の場合、係数は\( 2\)です!
「文字にかかっている数」を、係数と呼ぶ
例. \( 2x\)の係数は、\( 2\)

新しい言葉がたくさん出てきて混乱してきました、、

すみません、そうですよね、、
でも、これらはあくまで「言葉」にすぎないので、
「そういう言葉があるんだな」くらいで、そんなに真剣に考えなくて大丈夫です!
「言葉」を知っていれば、説明がしやすくで便利!という程度です。
では次に、この記事のメインとなる「1次式の例」について説明していきます!
1次式の例|2次式との違いは?

この章の冒頭で、
1次式とは、「文字1個のかけ算の項」までしか含まない数式
であると説明しました!

では、ここで質問です!
図中の1つ目の数式\( 2x+1\)は、「1次式」といえるでしょうか?

\( x \)という文字1つまでしか含んでいないので、「1次式」だと思います、、

正解です!
おっしゃる通り、図中の1つ目の数式\( 2x+1\)は、
まさに、文字\( x \)1個のかけ算の項までしか含んでいないため、1次式といえます!
一方、2つ目の数式\(x^2+ 2x+1\)は、
文字\(x\)2個のかけ算である\(x^2\)の項を含むため、1次式とはいえません!
このように、文字\(x\)2個のかけ算までを含む数式は、2次式と呼ばれます!
「文字2個のかけ算」までを含む数式を、2次式という

ここで問題です!
次のような数式は、何次式でしょうか?
\[ x+y+1 \]

文字が2個あるから、、2次式でしょうか?

残念ながら、不正解です、、難しいですよね、、
正解は、1次式です!
なぜなら、たしかに文字は2個ありますが、
「文字2個のかけ算をふくむ項」は無いからです!
この「文字どうしのかけ算があるかどうか」は、重要な違いとなります!

なるほど、、なんとなく分かってきた気がします、、
あと、細かい質問かもしれませんが、
「1次式」とか「2次式」という名前は、どこから来たんですか?

「次数」というモノと関係しています!
「次数」とは、1つの項の中で、かけ算している文字の個数です!
例えば、\(x\)の次数は1、\(x^2\)の次数は2です。
さらに、最も大きい次数が1である数式を1次式といいます!
「最も大きい次数が1」というのは、言い換えると、
「文字1個のかけ算の項までしか含まない」ともいえます。
これは、冒頭でした説明と同じですね!
また、同じように、
最も大きい次数が2である数式を2次式といいます。
あとは、3次式、4次式とかでも同じです!
「次数」とは、1つの項の中で、かけ算している文字の個数
ここまで、長かったですが、やっと本記事のメインテーマである、
1次式の場合での「たし算や引き算のまとめ方」を説明する準備ができました!
では、次から「1次式で、たし算や引き算をどうまとめるか」について説明していきます!
1次式の計算のやり方|同じ文字はまとめよう!
さっそく結論からいうと、この章で言いたいことは、
1次式において、「同じ文字をもつ項」は、
係数部分をたし算(ひき算)することで、
1つにまとめることができる
例. \( 2x+3x=5x \)
ということです!
要するに、「同じ文字をもつ項」は、まとめられるということです!
ここで、\( 2x \)と\( 5x \)のように、同じ文字をもつ項のことを同類項とよびます!
「同じ文字をもつ項」のことを、同類項と呼ぶ
さらに詳しく解説すると、1次式の計算方法の流れは、次のようになります!

上の図の例では、\(2x\)と\(4x\)が文字\(x\)を共通にもち、
\(4y\)と\(-2y\)が文字\(y\)を共通にもっていることが分かります。
図では、分かりやすいように、「同じ文字を持つ項」を近くにもってきています。
いったん、文字のことは忘れて、同類項の係数をたし算(ひき算)します。
図の例では、文字\(x\)を持つ項では、係数である2と3を足して5になり、
文字\(y\)を持つ項では、係数である4とー2を足して2になっています。
STEP2でいったんムシをした文字を、思い出して(元通りにくっつけて)計算は完了です。

でも、なんで同じ文字をもっていると、
まとめて計算ができるんですか?

気になりますよね、、
それについては、次の節で説明していきます!
なぜ、「同じ文字をもつ項」はまとめられるの?
「同じ文字をもつ項(同類項)は、係数部分をたし算すれば、まとめられる」
と急に言われても、納得できないですよね。
でも、大丈夫です!
「なぜ、まとめられるのか」は、次のポイントを頭にいれれば、簡単に理解できます!
かけ算は、「かけた数」個のたし算ともみなせる
例. \( 2\times 3 = 2+2+2 \)

もう少し詳しく説明すると、例としてあげた、\( 2\times 3 \)というのは、
「かけられている数(2)」が、「かけた数(3)」個ある
つまり
「2」を「3」回たし算している
というふうにも考えることができます!
また、\( 3\times 2 \)のときでも、
交換法則を使って、かけ算の順番をひっくり返すと、
\( 3\times 2 =2\times 3 \)とできるので、
同じように考えることができます!
要するに、
「かけられている数」も「かけた数」もひっくり返せるので、
かけ算の順番に関係なく、同じように考えられる
ということです!
「交換法則ってなんだっけ?」という方は、以下の記事をご覧ください!


「数字」を使ったかけ算のとき、
かけ算が、「かけた数」個のたし算ともみなせる
ということは、なんとなく理解できました!
でも、これは「文字式」のときも同じことがいえるのでしょうか?
イメージがつきません、、

おっしゃる通り、「文字式」についても同じことがいえます!
なぜなら、「文字」といっても、
その中身は、けっきょくのところ「数字」だからです!
例えば、\( x\times 3 \)というのも、
「かけられている文字\(x\)」が、「かけた数(3)」個ある
つまり
「\(x\)」を「3」回たし算している
というふうにも考えることができます!
これを数式にすると、\( x\times 3 =x+x+x\)となります!
また、交換法則があるため、
\( x\times 3 = 3\times x \)というふうに、かけ算をひっくり返すことができ、
\( 3\times x =x+x+x\)と表すこともできます!

以上のことを頭に入れたうえで、
例として、\( 2x+3x\)という1次式を考えてみましょう!
\( 2x+3x\)
これまで説明してきた、
かけ算は、「かけた数」個のたし算ともみなせる
というポイントを頭にいれると、上の1次式は、次のように考えることができます!
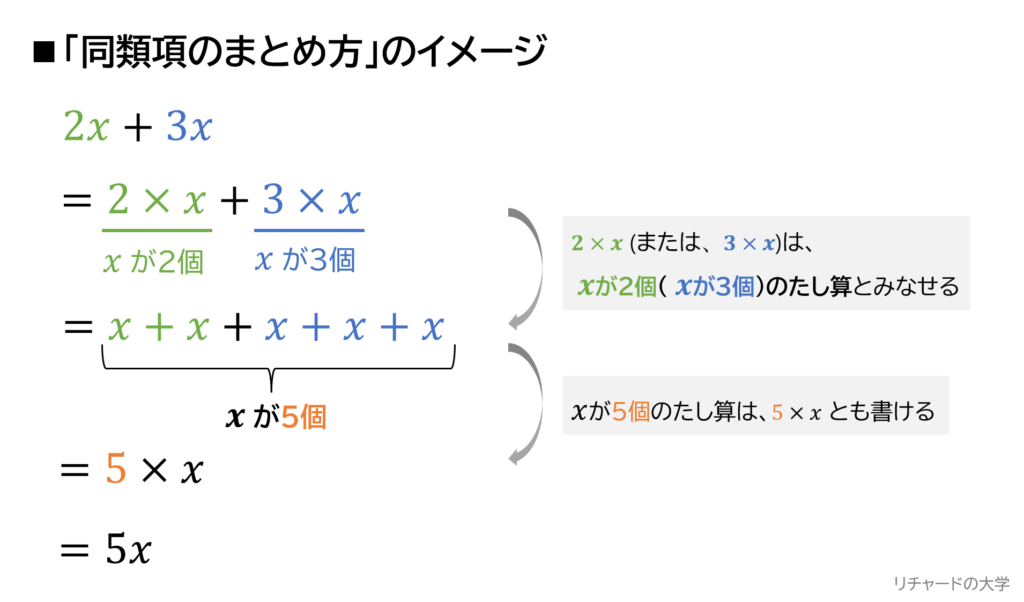
\( 2\times x\)(または、\( 3\times x\))というのは、
これまで説明してきた「かけ算とたし算の関係」を使うと、
\( x\)が2個たし算されている(または、\( x\)が3個たし算されている)
というふうにも考えられます。
よって、\( 2\times x\)や\( 3\times x\)という「かけ算」は、
どちらも「たし算」の形にすることができます。
STEP1によって、全ての「かけ算」がほぐされて、
\( x\)2個のたし算と\( x\)3個のたし算が生まれました。
これらをまとめると、\( x\)5個のたし算と見なすことができます。
\( x\)5個のたし算というのは、「かけ算とたし算の関係」を考えると、
\( x\times 5\)という「かけ算」とみなすことができます。
さらに\( x\times 5\)を\( 5x \)と省略すれば、完成です!
少しまわりくどく感じたかもしれませんが、以上が、同類項のまとめ方のイメージです!

ここで重要な点は、
文字式である\( 2x \)や\( 3x \)というのは、
係数(2または3)個の\( x \)のたし算とみなせる点です!
さらに、\( x \)のたし算をまとめる(かけ算とみなす)ことで、
同類項である\( 2x \)や\( 3x \)を、
\( 5x \)という1つの項にまとめることができました!
まとめると、
文字式は、「係数個のたし算」とみなせるため、
係数部分をたし算することで、同類項は1つの項にまとめることができる
ということになります!
同類項は、係数部分をたし算することで、
1つの項にまとめられる
まとめ|最低限覚えてほしいこと
この記事では、
- 1次式とはなにか
- 「同類項」の具体的なまとめ方
- 「同類項」をまとめられる理由
について解説しました!
「1次式」とは、
「文字1個のかけ算の項」までしか含まない数式
でしたね。また、「同類項」とは、
「同じ文字をもつ項」のこと
でした。さらに、「同類項」の具体的なまとめ方の結論は、
1次式において、「同類項」は、
係数部分をたし算(ひき算)することで、
1つにまとめることができる
例. \( 2x+3x=5x \)
ということでしたね。
なぜ、このように「同類項」をまとめられるのかというと、
文字式は、「係数個のたし算」とみなせるため、
係数部分をたし算することで、
同類項は1つの項にまとめることができる
ということでした!

今回の内容は、
「項」や「1次式」など、新しく出てきた言葉が多くて、大変でした、、

おっしゃる通り、新しい言葉が多かったですね、、
ただ、今回ご紹介した言葉は、これからもよく使う重要なものになるので、
ぜひ、使いながら覚えていきましょう!
また、「同類項のまとめ方」や「同類項をまとめられる理由」の解説では、
少し遠回りぎみな話も多かったかもしれませんが、
なんとなくのイメージをつかんでもらえたならば嬉しいです!
なお、これから先で「因数分解」というものを学習すれば、
「なぜ、同類項はまとめられるのか」がさらによく理解できると思います!
これからも、イメージを大切にしながら、数学の学習を進めていきましょう!
ここまでお読みいただきありがとうございます。
この記事がどなたかのお役に立てれば幸いです。
参考文献
この記事を書くにあたっては、以下の書籍も参考にしています。
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい!」
という学生や社会人の方に、非常におすすめです!
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という面では、本ブログに分があると思うため、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです!
その理由は、次の通りです!
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です!
14日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓