正負の数のたし算(加法)を「すごろくのイメージ」と「最低限理解すべき4つの例題」でわかりやすく解説!【中1数学・正負の数②】
この記事では
- 正負の数のたし算(加法)ってどうやるんだっけ?復習したい!
- 正負の数のたし算(加法)を学校で習ったけど、
「なぜ、そういうふうにたし算できるのか」がよくわからなかった、、
という方のために、この記事では、
- 「正負の数のたし算(加法)」のやり方の要点
- 最低限理解すべき4つの例題
- なぜ、そのようにたし算できるのか
について、すごろくを使ったイメージを中心にして、わかりやすく説明していきます。
イメージを通して本質が理解できるように説明していきますので、
この記事を読むことで、
「正負の数のたし算(加法)」に関するどんな問題に対しても通用する基礎
を身に着けることができます!
といっても、
まずは計算ができることが大切ですので、
最初に「正負の数のたし算のやり方」についてまとめた後、
「最低でも理解すべき4つの例題」をとおして、
「なぜ、そのやり方でたし算ができるのか」について解説していきます。

それでは、始めていきましょう!
この記事の内容は、動画でも公開しています!
「文字よりも、動画の方がはかどる!」という方は、ぜひご覧ください!
また、私も頑張って動画をつくってはいますが、やはりプロの講師には勝てません、、
プロの講師で学べる教材の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です!
14日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓
「正負の数のたし算(加法)」のやり方
さっそくですが、正負の数のたし算のやり方についてまとめます。


すみません、たし算のやり方は分かったのですが、
なぜそんなやり方で、たし算ができるんですか?

それについては、次の節で、
「最低でも理解すべき4つの例題」と
「すごろくのイメージ」を交えながら説明していきます!
「最低でも理解すべき4つの例題」を、すごろくのイメージで解説
「なぜ、前述したやり方で、正負の数のたし算が計算できるのか」を理解するために、
次の4つの例題をみていきましょう!
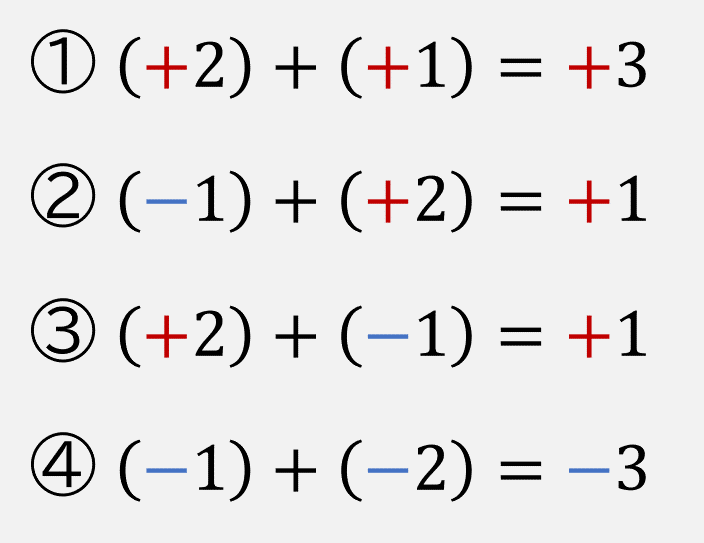
上の例題をみると、小学生のときにやった足し算とは、全然違うように思えて、
少しとまどいますよね。
ただ、小学校までの「数」と同じように、
正負の数を使ってもたし算ができるということはわかると思います。
さらに、実は、上の4つの例題は、
「正負の数のたし算(加法)」で出てくる問題のパターンをすべて含んだ例題になっています。
つまり、この4つの例題を理解すれば、正負の数のたし算はバッチリというわけです!
そういうわけで、これから、上の4つの例題について
「イメージすること」を大事にしながら、くわしく説明していきます!
【例題1】正の数どうしのたし算(加法)
\( (+2) + (+1) = +3 \)
例題1は、正の数である+2と、正の数である+1でのたし算です。
この計算をイメージするために、
前回の記事に引き続き、すごろくの例を使って説明していきます。
下の図では、現在地を車の駒(人生ゲームをイメージ)で表し、
例題1のたし算を、すごろくの駒の動きで表しています。
まず重要なポイントとして、すごろくの例では、
「たし算」は「車のこまを前へ進めること」
だと考えることができます。
すごろくのイメージにおいて、
「たし算」は、「車のこまを前へ進めること」
具体的に、例題1ではどのようなイメージになるのかを見ていきましょう。
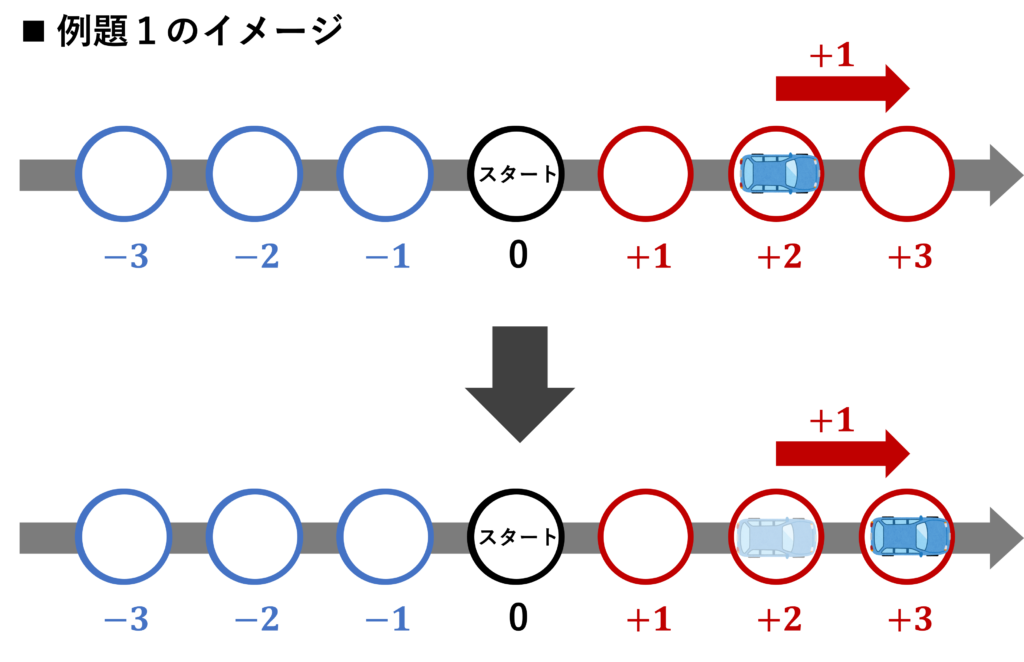
例題1をすごろくでのイメージで考えると、
\( (+2) + (+1) \) のたし算は、
「いま自分がいるマス(例題では、+2)から、
足した数(例題では+1)だけのマスを前へ進むこと」
だと考えられます。
なぜなら、例題1のたし算というのは、
「+2よりも+1だけ大きい数を求めること」だからです。
つまり、すごろくを使った、例題1のイメージは、以下のようになります。
「たし算が行われる前の数」は、+2です。
最初の位置(+2)に対して、+1のたし算が行われます。
(+2)+(+1)のたし算の結果、+3になりました。
以上をまとめると、次のようになります。
最初は(+2)にあった車が、
+1マス分進み
(+1のたし算が行われて)、
(+3)のマスに到着
これが、すごろくを使ったときの、たし算のイメージです。

ちょっと待ってください!
これって、結局、
小学生の時にやった足し算と同じじゃないですか?

おっしゃる通りです!
「正の数どうしのたし算」は、
小学校までに使ってきた「数」の時と、やり方が同じになります。
このことは、
「正の数」は、小学校までに使ってきた「数」と同じものである
ということを思い出せば、すんなり理解できると思います。
つまり、正の数どうしのたし算は、小学校までにやった足し算となにも変わりません。
正の数どうしのたし算は、
小学校までと同じように計算すればよい
なぜわざわざ、そんな簡単な問題を、すごろくの例を使って説明したかというと、
負の数が入った時のたし算でも、同じようなイメージをもってほしかったからです!
今回紹介したすごろくのイメージを大切にして、
次からは、「正の数と負の数のたし算」について説明します!
【例題2】正の数と負の数のたし算(加法)①
例題2は、正の数である+2と、負の数であるー1でのたし算です。
\( (-1) + (+2) = +1 \)
なぜ例題のように計算できるのかをイメージするために、
例題1のときと同じように、すごろくの例を使って説明します!

上の図は、例題1と同じように、車があるところが、現在地のマスを表しています。
例題2では、(-1)+(+2) という足し算をしていますが、
これをすごろくの例でイメージすると、次のようになります。
「たし算される数」は、ー1です。
最初の位置(ー1)に対して、+2のたし算が行われます。
(ー1)+(+2)のたし算の結果、+1になりました。
以上のことは、次のようにまとめられます。
最初は(ー1)にあった車が、
+2マス分進み
(+2のたし算が行われて)、
(+1)のマスに到着
これは、出発点が,、負の数である(ー1)となるだけで、
やっていることは、例題1のときと変わらないことがわかります。
(例題1では、出発点が(+2))
では、例題3の場合だとどうでしょうか。
【例題3】正の数と負の数のたし算(加法)②
\( (+2) + (-1) = +1 \)
例題3でも、これまでと同じように、まずは(+2)からスタートします。
しかし、これまでと違う点は、たす数が「負の数」であることです。
前回の記事でもご説明したように、
負の数を使うと、「反対の向き」を考えることができるのでした。
つまり、負の数をみたときには、
正の数の場合に対して、反対のことを考える必要があります。
具体的には、正負の数のたし算(加法)で、
「負の数を足す」ときには、
「正の数を足す」ときとは、反対方向に、たし算をすることになります。
これが、例題3における最重要ポイントです。
「負の数を足す」ときには、
「正の数を足す」ときとは、反対方向に、たし算をする
といっても、まだよくわからないと思うので、次のすごろくの例をみてみましょう。

すごろくの例では、例題3のイメージは以下のようになります。
「たし算される数」は、+2です。
車を反対向きにする
「負の数を足す」というのは、
「正の数を足す」のとは真逆のことをします。
つまり、「負の数を足す」ときは、
「正の数を足す」ときと反対方向に、たし算をすることになります。
+1マスぶん、前に進む
最初の位置(+2)に対して、+(ー1)のたし算が行われます。
(+2)+(ー1)のたし算の結果、+1になりました。
以上のステップをまとめると、次のようになります。
- スタートは(+2)であるため、
車はまず(+2)マスにいる - 「たす数」にー(マイナス符号)が付いているため、
(「たす数」が負の数であるため)
車を反対向きにする - 反対向きのまま、
車を(+1)マス前に進める
(+(ー1)のたし算を行う)
冒頭でも説明しましたが、例題3で最も重要なことは、
「負の数を足す」ときには、
「正の数を足す」ときとは、反対方向に、たし算をする
ということです。

負の数を足すときのイメージは、なんとなく分かりました!
ただ、+(プラス)符号って、省略してもいいんでしたよね?
そしたら、例題3は、\( 2 -1 = 1 \)となって、
小学校でやったような、ただのひき算になっちゃいませんか?

おっしゃる通りです!
しかし、なぜ、こんなただの引き算を、
例題3のように、正負の符号をつけた形で書いたかというと、
引き算に対する新しい考え方を知ってほしかったからです。
それは、
「正の数を引くこと」は、「負の数のたすこと」に等しい
ということです。

おっしゃる通りです!
しかし、なぜ、こんなただの引き算を、
例題3のように、正負の符号をつけた形で書いたかというと、
引き算に対する新しい考え方を知ってほしかったからです。
それは、
「正の数を引くこと」は、「負の数のたすこと」に等しい
ということです。
これについては、次で詳しく解説していきますが、
補足となるので、読み飛ばしてもらっても大丈夫です!
【例題3の補足】すべてはたし算とみなせる?

前の節で、
「正の数を引くこと」は、「負の数のたすこと」に等しい
という文言が出てきましたが、この段階では、意味不明ですよね、、
そこで、次から少し例を挙げながら説明していきます!
例として「テストの点数が、5点下がった」ことを、親へ報告する状況を考えてみましょう!
普通は、「+5」という正の数をつかって、
「テストの点数が、+5点下がった」
と報告するのが普通ですよね。

でも、親へ報告するときは、
あんまり「下がった」って言いたくないよな、、

そうですよね、、
ここでは、なるべくポジティブな印象を親へ与えるために、
「上がった」という表現を使いたいところですよね、、
その場合、どうしたらよいでしょうか?
実は、「ー5」という負の数を使うことで、
「テストの点数が、+5点下がった」というネガティブな表現を、
「テストの点数が、ー5点上がった」というポジティブな表現へ変換することができます!
要するに、
「テストの点数が、+5点下がった」=「テストの点数が、ー5点上がった」
というわけです!
「下がった」というのは、「ひき算」、
「上がった」というのは、「たし算」としても考えられるため、
「正の数を引くこと」=「負の数をたすこと」
ということもできます!
「正の数を引くこと」は、
「負の数をたすこと」に等しい
また、例題2と例題3からわかるように、
\( (-1) + (+2) \) と \( (+2) + (-1) \) の答えは同じ\(+1\)になります。
このことは、例題2と例題3はどちらも、
正の数と、負の数をたし算している
という見方をすれば、あたりまえに思えてくるはずです。
このように、これから先、数学を勉強していくうえでは、
引き算を、負の数を使った、たし算とみなすこと
が重要となります!
なぜなら、次回の「正負の数のひき算(減法)」の記事でも説明するように、
「ひき算を、すべてたし算とみなす」ことで、
数式をみたときに、たし算なのかひき算なのかを、いちいち考えずに済すむからです。
つまり、
頭の中を整理し、数式をより簡単に考えるために、
「ひき算を、負の数のよるたし算とみなすことで、全てたし算に統一する」
というわけです。
【例題4】負の数どうしのたし算
\( (-1) + (-2) = -3 \)
最後に、例題4ですが、これは例題3と同じ考え方がつかえます。
例題3と同じように、すごろくを使ってイメージすると、次の図のようになります。

例題4は、すごろくのイメージを使うと、次のステップで考えることができます。
「たし算が行われる前の数」は、ー2です。
車を反対向きにする
「負の数を足す」というのは、「正の数を足す」のとは真逆のことをします。
つまり、「負の数を足す」ときは、
「正の数を足す」ときと反対方向に、たし算をすることになります。
2マスぶん、前に進む
最初の位置(ー1)に対して、+(ー2)のたし算が行われます。
(ー1)+(ー2)のたし算の結果、ー3になりました。
以上のステップをまとめると、次のようになります。
- スタートは(ー1)であるため、
車はまず(ー1)マスにいる - 「たす数」にー(マイナス符号)が付いているため
(「たす数」が負の数であるため)、
車を反対向きにする - 反対向きのまま、
車を(+2)マス前に進める
(+2のたし算を行う)
このイメージは、例題3のときと同じですね。
違っていることは、スタート地点が負の数(ー1)だということだけです。
また、結果をみると、
「負の数どうしのたし算」は、ー(マイナス)符号を無視すると、
小学校までにやった足し算とおなじように計算できることがわかります。
「正の数どうしのたし算」との違いは、
最後の計算結果に、ー(マイナス)符号をつけるかどうかだけですね。
負の数どうしのたし算は、
ー(マイナス符号)を無視して、単純にたし算し、
最後の結果に、ー(マイナス符号)をつければよい
これから先、計算していくときには、
この考え方をつかうのが1番はやいので、覚えておきましょう!
まとめ|「正負の数のたし算」の重要ポイント
この記事では、
- 「正負の数のたし算(加法)」のやり方の要点
- 最低限理解すべき4つの例題
- なぜ、そのようにたし算できるのか
について解説しました。
今回の記事において、最低でも覚えて帰ってほしい重要ポイントは、以下の3点です!

これらは、全て記事内でご説明したポイントですね。
特に2つ目のポイントは、
次回で説明する「正負の数のひき算(減法)」でも重要となりますので、
ぜひ頭にいれておいてください!
最後までお読みいただき、ありがとうございます。
この記事が、どなたかの助けになれれば幸いです。
次回の記事では、「正負の数のひき算(減法)」について説明していきます!
こちらの記事でも、要点をしぼり、「すごろくのイメージ」を使って、
直感的に理解できるように解説していますので、是非ご覧ください!
参考文献
この記事を書くにあたっては、以下の書籍も参考にしています。
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい!」
という学生や社会人の方に、非常におすすめです!
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という面では、本ブログに分があると思うので、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです!
その理由は、次の通りです!
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です!
14日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓