「正負の数・絶対値とはなにか」や「負の数のメリット」を、すごろくのイメージで、わかりやすく解説!【中1数学・正負の数①】
- 「正の数・負の数」って何?どんなルールで決まってるんだっけ?
- 「正の数・負の数」のイメージがつかめない、、
- 「正の数・負の数」って、けっきょく、なんの役にたつの?
- 「絶対値」ってなんだっけ?
そんな方のために、この記事では、
- 「正の数・負の数」を決めている、3つのルール
- 「正の数・負の数」を使う2つのメリット
- 「絶対値」とはなにか
- 「絶対値」をつかうメリット
について、すごろくのイメージを使って、わかりやすく説明していきます!
この記事を読むことで、
「正の数・負の数」の直感的なイメージがつかめるため、
今後の学習にも応用できるような、本質的な理解を得ることができます!

それでは、始めていきましょう!
この記事の内容は、動画でも公開しています!
「文字よりも、動画の方がはかどる!」という方は、ぜひご覧ください!
また、私も頑張って動画をつくってはいますが、やはりプロの講師には勝てません、、
プロの講師で学べる教材の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です!
14日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓
正の数・負の数とは?|3つのルール
正の数・負の数というのは、
「数の世界」をさらに広げるため、新たに決められた「数」の考え方です。
具体的には、次のような3つのルールで決められています。

・プラス記号(+)は、省略できる!
・マイナス記号(ー)は、省略できない!

小学校で習った「数」とはぜんぜん違って、難しそうですね、、

確かに、上のルールだけをみると、複雑に見えますよね。
でも、大丈夫です!
小学校で習った「数」との違いは、
新たに「負の数」という数が入ってきたことだけです!
「正の数」というのも、
小学校で習った「数」そのものにすぎません!
また新たに入ってきた「負の数」という数も、
足し算や引き算、掛け算、割り算ができるため、
本質的には、小学校で習った「数」と同じです!

そう言われても、「負の数」は、身の回りでは全然見ませんし、
どういうものなのか、あまりピンとこないです、、

確かに、「負の数」はあまり身近なものではないですよね。
理解するためには、慣れが必要だと思います。
ですが、負の数というのは、高校や大学などで、
これから先も長く付き合っていく重要な「数」です!
そこで、まずは、すごろくの例を使って、
直感的なイメージをつくり、少しずつ慣れていきましょう!
正の数・負の数を、すごろくでイメージ!
正の数・負の数をイメージするために、次のようなすごろくの例を考えてみましょう。
小学校までの「数」のイメージ|正の数
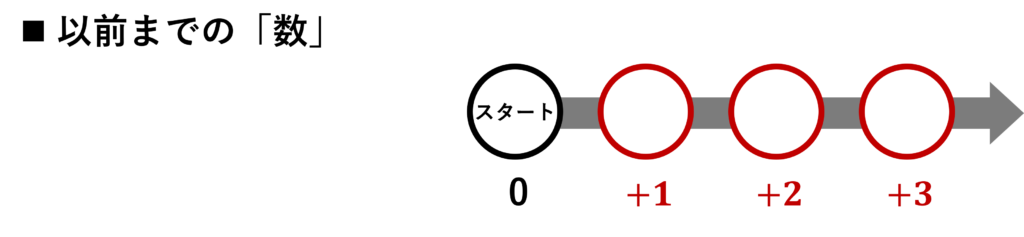
このすごろくでは、
小学校までにならった「数」の範囲
を表しています。
このすごろくは、
0のマス(基準点)に対して、
片側の範囲内のみ、コマを動かせる
普通のすごろくです。
コマは、片側の範囲のみを動くため、
進むときは必ずスタート(基準点)をゼロとして、
+1マス、+2マスとコマをすすめていきます。
プラス記号は省略できるため、
表せる「数」としては、1、2、3といった具合です。
これはちょうど、小学校までに使っていた「数」の範囲そのものですよね。
小学校までの「数」の範囲を、すごろくで例えると、
スタート(基準点)をゼロとして、
片側の範囲のみ、コマを動かせるすごろく
とみなせる

では次に、中学校から使う「数」は、どんなイメージになるのかを説明していきます!
中学校からの「数」のイメージ|正の数・負の数
小学校の「数」のすごろくに対して、
中学校の「数」のすごろくは、
次の図のように、
コマが、スタートのゼロ(基準点)から後ろへも進めるような、変なすごろくです。
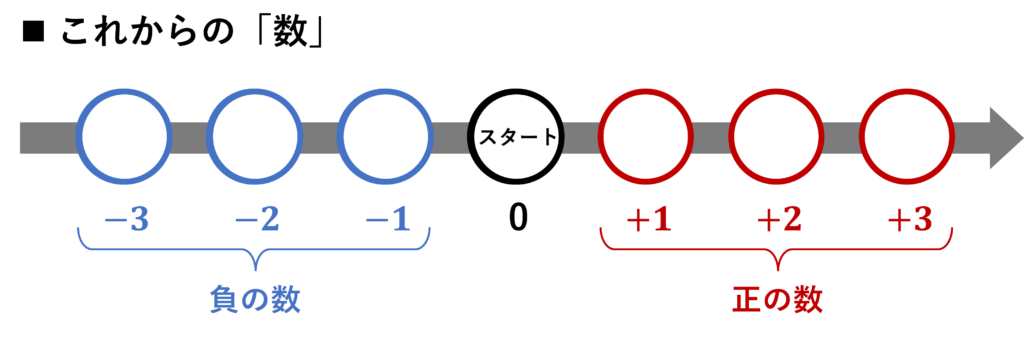
コマを「スタート(ゼロ)の後ろ」にも進めるためには、
小学校までに使ってきた「数」(1, 2, 3など)だけでなく、
「スタート(ゼロ)よりも後ろ」を表す新たな「数」を考える必要があります。
そこで、スタートをゼロとして、
「-(マイナス)という記号をつけた数」を新たに考えます。
これが、負の数です。
こうすることで、スタート(ゼロ)から始まって、
1マス後ろのマスを、ー1マス、2マス後ろのマスを、ー2マスというように、
「スタート(ゼロ)に対して、反対側のコマの位置」を考えることができるようになります!
これは、小学校までの「数」では、出来なかったことです!
負の数を、すごろくの例でイメージすると、
スタート(ゼロ)に対して、反対側(後ろ側)のコマの位置
とみなせる。

でも、そもそもなぜ、
スタート(ゼロ)の反対側を考える必要があるんですか?

また、負の数という新たな数を考えてしまったため、
これと区別するために、これまで使ってきた、1,2などの普通の数にも、
+(プラス)という記号をつけることがあります。
これを正の数と呼びます。
正の数は、すごろくの例において、
スタート(ゼロ)に対して、前側のコマの位置
と考えることができます!
正の数は、すごろくの例でイメージすると、
スタート(ゼロ)に対して、前側のコマの位置
とみなせる。

そしたら、正の数というのは、けっきょく、
小学校で使っていた「数」と同じものということですか?

おっしゃる通りです!
名前が変わっただけで、
正の数は、小学校で使っていた「数」そのものなので、
正の数の使い方は、
これまで使ってきた「数」と何も変わりません!
実際、これから先(高校・大学以降)でも、
プラス記号(+)は、ほとんど省略して使います。
ただ、今回のように、負の数と区別するために、
あえてプラス記号(+)をかくこともあるため、
「そういう書き方ができるんだなー」くらいで覚えておくといいかもしれません!
こうすることで、スタート(ゼロ)から始まって、
後ろに1マス進むことを、ー1マス、後ろに2マス進むことを、ー2マスというように、
「スタート(ゼロ)に対して後ろ向きに進むマスの数」を考えることができるようになります。
これは、今までの「数」では、出来なかったことです。
つまり重要なことは、
スタートであるゼロを目印として、負の数を使うことで、
これまで使ってきた「数」とは、反対向きの「数」
を考えられるようになった
ということです!
「負の数」を使う2つのメリット
「負の数なんていう変な数を使うことのメリットって何があるんだろう?」
と疑問に思いますよね。
筆者の考える「負の数を使うメリット」は次の2つです!
- 「ある基準よりも小さい数」を表せる
- 「正反対のこと」を表せる
メリット1つ目|「ある基準よりも小さい数」を表せる
まず1つ目ですが、この例としては学校のテストの点数が挙げられます。

学校のテストの結果が出て、まず気になるのは何でしょうか?

やはり、まず、平均点が気になります!
自分の点数が平均点より上だとほっとしますし、
逆に、平均点より下だと悲しくなります、、

そうですよね、、
また、自分の両親に点数をつたえる時も、平均点は重要です。
例えば、自分の点数が39点だったとしても、
平均点が40点だったことも同時に伝えれば、
怒られることはないでしょう(家庭によるかもしれません)。
このように日常生活の中では「平均点よりも1点低かった」と伝えれば十分ですが、
例えば、学校の先生は、「生徒の点数の出来」を記録する必要があります。
その際、「平均点よりも1点低かった」という記録のつけ方よりも、
「何らかの数値」で記録をとったほうが、あとで計算を行う際などにとても便利です!
このとき、負の数が力を発揮します!
つまり、「平均点よりも1点低かった」ではなく、
負の数を使うことで、「平均点をゼロとしたとき、ー1点だった」
というふうに、平均点(基準)より小さい点数を、「数」で正確に記録できます!
このように、平均点などの「基準」があるとき、
負の数を使うことで、その基準よりも小さい数を表せる
というのが負の数のメリットの1つです!

あ、さっきのすごろくの例で、スタート(ゼロ)という基準よりも、
後ろ側(ゼロより小さいマス)へコマを動かせた
というのも、これと同じことですよね!

おっしゃる通りです!
負の数を使うことで、
「ある基準より小さいもの」を
「数」で表すことができる!
メリット2つ目|「正反対のこと」を表せる
2つ目のメリットの例としては、先ほどのすごろくが挙げられます。
正の数だけでは、「コマが前方向に進むこと」だけしか表せませんでした。
例えば「前に1マス進むときは+1マス、前に2マス進むときは+2マス」
といった具合です。
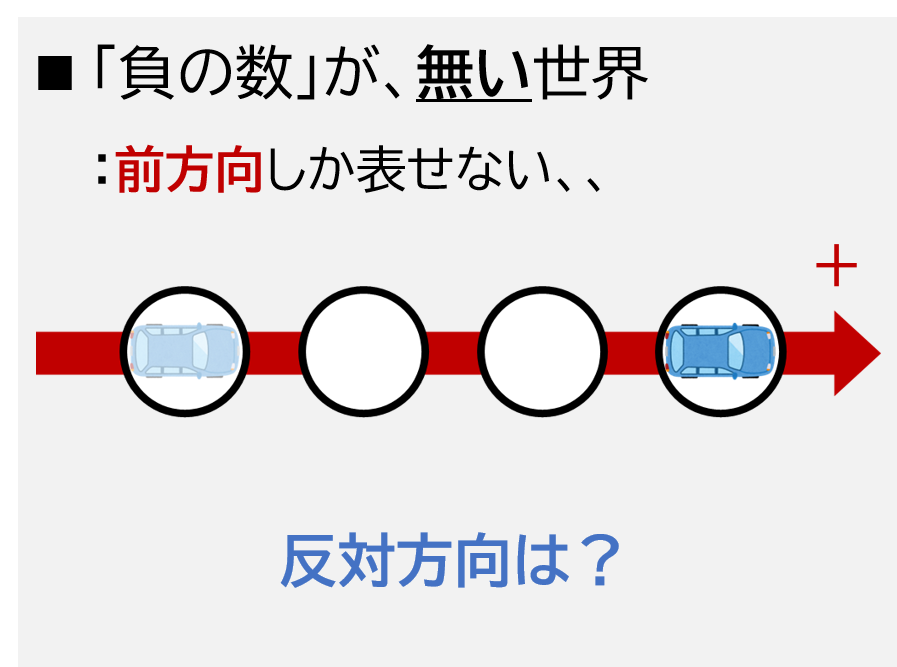
一方、負の数を使うことで、
「後ろに1マス進むときはー1マス、後ろに2マス進むときはー2マス」というように、
「後ろ方向に進むこと」も表せるようになります!
このように、ある事柄(前方向に進む)に対して、
「正反対のこと(後ろ方向に進む)を表せる」
というのが、負の数の大きなメリットです!
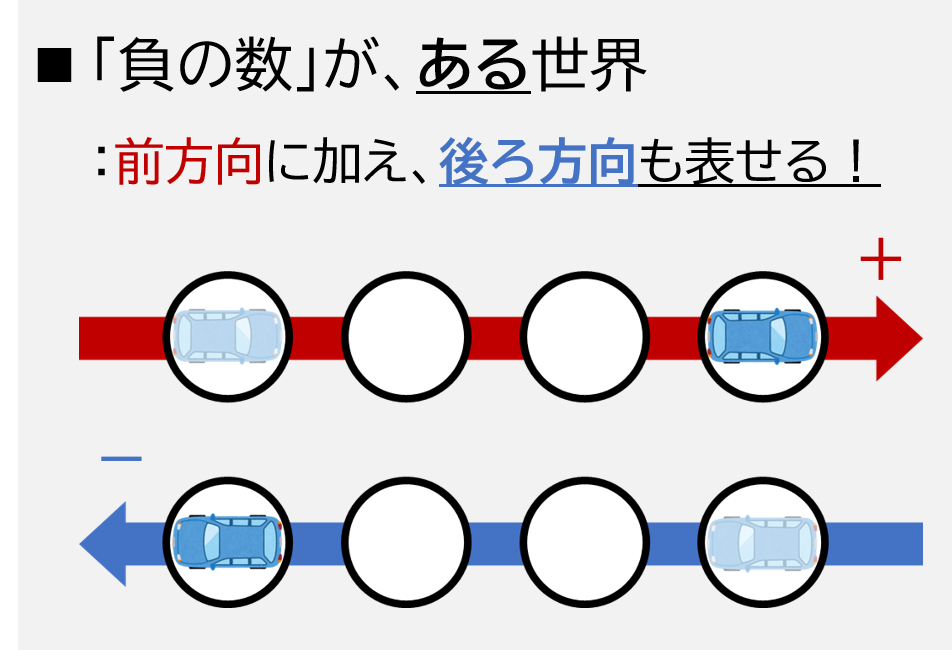
負の数を使うことで、
「ある事柄に対して、正反対のこと」を表せる!

でも、「正反対のことを表せる」というのは、
そんなに重要なんでしょうか?

重要です!
なぜなら、身の回りには、意外と「正反対のこと」が存在するからです!
例えば、「方向」がよい例です!
ある方向に進んでいる車が、
ちょうど反対向きに進む(バックする)とき、
そのバックする方向を表すにはどうしたらよいでしょうか?
正の数しかない場合は難しいですが、
負の数を使うと、進んでいる方向に対してー(マイナス)符号をつける(負の数に変える)だけで、
ちょうど正反対の方向を表すことができます!
負の数をつかうことで、
身の回りにある「反対向き」
まで考えられるようになる!

では、最後に、
重要な用語である「絶対値」について解説していきます!
絶対値ってなに?
絶対値って、言葉だけ聞くとなんだか難しそうですよね、、
でも、中身は大したことないので大丈夫です!
さっそくですが、結論からいうと、
絶対値とは、
ゼロ(基準点)から、どれだけ離れているか
(ゼロからの距離)
例. +3の絶対値は3、ー3の絶対値は3
のことをいいます。

すみません、これだけだとよくわかりません、、

そうですよね、、やはり言葉だけではピンとこないですよね。
そこで、ふたたびすごろくの例をつかって、
イメージをつくっていきましょう!
次の図は、ー3と+3を、すごろくのコマ(車)の位置で表したイメージです!

車のコマは、ー3と+3の場合では、それぞれ全く正反対の位置にいることがわかります。
しかし、スタート(ゼロ)からの距離を考えてみると、
どちらも同じ「3」だけ離れています!
この「ゼロからの距離」のことを、「絶対値」といいます!
すごろくでイメージすると、
絶対値とは、スタート(ゼロ)からの距離
とみなせる!

言葉だけだとよく分かりませんでしたが、
すごろくで考えると、なんとなくイメージがつかめてきました!

よかったです!
絶対値という言葉は、これからよく使うため、
イメージだけでもつかめると、今後が楽になります!

そういえば、そもそも「絶対値」ってなんの役に立つんでしょうか?

やはり気になりますよね、、
それについては、次の章で説明していきます!
絶対値をつかうメリットは?
結論から言うと、絶対値を使うメリットは、
ある基準点からの「ズレ」の大きさを表せる
ことです!

すみません、ぜんぜんピンとこないです、、

そうですよね、、
それでは、例を使って説明していきましょう!
例としては、バスの来る時刻を考えてみます。
電車と違い、バスって遅れてくることが多いですよね、、

そうですね、、遅れてくるだけでなく、時刻表の時間よりも早く来ることもあります、、

そうですよね、、どちらにせよ、
時刻表と、実際のバスの到着時刻に「ズレ」があると困りますよね。
なるべく、「ズレ」が少ないバスに乗りたいところです。
では、どうやれば、「ズレ」の少ないバスを見つけることができるでしょうか?

なにか、「ズレ」の大きさみたいなもので、比較するとかですかね、、?
あ!そのときに、「絶対値」が使えるのか!!

おっしゃる通りです!

例として、上の図のようなバスを考えてみましょう!
12/23は、予定時刻(12:00)よりも20分遅れてきました。
(予定時刻を基準点とすると、+20分)
これを、絶対値(基準点からどれだけ離れているか)で考えると、20という値になります!
一方、12/24は、予定時刻(12:00)よりも10分早くきました。
(予定時刻を基準点とすると、ー10分)
これを絶対値で考えると、10という値になります!
(※基準点からのズレの大きさは、正の数も負の数も関係ない!)
同様に、5分遅れて到着(+5分)した12/25についても、
絶対値を考えると、5という値になります!
3日間で絶対値を平均すると、
(20+10+5)÷3=11.6666…となり、約12という値を得られます!
つまり、今回の例で考えたバスは、
平均して約12分の「ズレ」で到着するということになります!
なかなかの「ズレ」ですよね、、
例えば他に、平均して5分の「ズレ」(ズレの絶対値が5)で到着するバスがあった場合、
迷わずそちらに乗る方が得策ということになります!
このように、絶対値をつかうことで、
ある基準点(今回の場合は、時刻表)からのズレの大きさを、数値であらわし、
比較などの様々な分析が可能となります!
まとめ|「正負の数の要点」と「メリット」
この記事では、
「正負の数とはなにか」や「負の数を考えるメリット」について解説しました!
最低でも覚えて帰ってほしいポイントは、次のとおりです!

負の数というのは、あまりなじみのない考え方のため、慣れるまで大変ですよね、、
ですが、これからもたくさん関わっていきますので、少しずつ慣れていきましょう!

これからも、負の数はたくさん使うんですね、、頑張ります!
そういえば、正の数は、小学校で習った「数」と同じように、
たし算や引き算ができると言っていましたが、
負の数のときは、どうやればいいんですか?

負の数のときも、たし算や引き算は可能です!
ただ、小学校までの「数」とは、扱い方が違ってくるため、
次の記事で詳しく解説します!
次回は、「正負の数のたし算(加法)」について、解説していきます!
数式だけでの理解は難しいですが、
今回と同様に、「すごろくのイメージ」を使って、
直感的に理解できるように説明していますので、ぜひご覧ください!
参考文献
この記事を書くにあたっては、以下の書籍も参考にしています。
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい!」
という学生や社会人の方に、非常におすすめです!
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という意味では、本ブログに分があると思うので、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです!
その理由は、次の通りです!
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です!
14日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓