１次式ってなに？「同類項のまとめ方」や「なぜ、まとめられるのか」についてわかりやすく解説！【中１数学・文字と式③】
リチャード
リチャードの大学
【正負の数のひき算(減法)】すべてのひき算は、たし算とみなせる？２つの要点を「すごろくのイメージ」でわかりやすく解説！【中１数学・正負の数③】
リチャード
この記事では、
- 「正負の数のひき算」の復習のために、要点をしりたい！
- 「正負の数のひき算」を学校でならったけど、
「なぜそうなるのか」のイメージがよくわからない、、
という方のために、
- 最低限しっておくべき
「正負の数のひき算」の２つの要点 - 最低でも理解すべき２つの例題
- 「正負の数のひき算」の
本質を理解するためのイメージ
について、すごろくのイメージを使って、わかりやすく解説していきます！
イメージを使うことで、本質が理解しやすくなるため、
この記事を読むことで、
「正負の数のひき算(減法)」に関するどんな問題にも通用する基礎を
身に着けることができます！
それでは、始めていきましょう！
この記事の内容は、動画でも公開しています！
「文字よりも、動画の方が理解しやすい！」という方は、ぜひご覧ください！
また、私も頑張って動画をつくってはいますが、やはりプロの講師には勝てません、、
プロの講師で学べる教材の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です！
１４日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓
Contents
「正負の数のひき算」の２つの要点
さっそく、要点を教えてください！
すみません、要点を紹介したいのはやまやまなのですが、
少し抽象的でわかりずらいので、
まず、今回の記事をとおして、何をしたいのか（目標）をお伝えします！
それは、
すべての「ひき算」を、「たし算」へ変換したい
ということです！
言い換えると、
なるべくひき算を考えずに、たし算だけしたい！
ということになります！
それをふまえた上で、「正負の数のひき算」の要点２つは、以下となります。
といっても、まだよくわからないですよね。
そこで、次の節では、
「最低でも理解すべき２つの例題」と「すごろくのイメージ」を使って、
「正負の数のひき算」の要点について、くわしく解説していきます！
「最低でも理解すべき２つの例題」を、すごろくのイメージで解説！
この節では、次の２つの例題を解説していきます。
実は、この２つの例題は、
「正負の数のひき算(減法)」に現れる問題のパターンをすべて含んだものになっています。
つまり、この２つの例題を理解すれば、「正負の数のひき算」はバッチリというわけです！
それでは、１つずつ見ていきましょう！
【例題１】正の数をひく
例題１
\( (+2) – (+1) = +1 \)
【例題１】「正の数をひくこと」は、「負の数をたすこと」と同じ
前回の「正負の数のたし算(加法)」の記事を読んだ方の中には、
「この例題みたことある！」と思った方もいらっしゃると思います。
実は「正負の数のたし算」の記事における例題３の
\[ (+2) + (-1) = +1 \]
という計算と、今回の例題１でやっていることは、本質的に全くおなじです。
なぜなら、前回の「正負の数のたし算」の記事でお話しした、
「正の数をひくことは、負の数をたすことと同じ」という重要な考え方が、
この例題１にもあてはまるからです。
例をあげると、
「テストの点数が+５点落ちた」と、「テストの点数がー５点上がった」
は、結局は同じことを言っていますよね。
（ー５点上がったとは、言わないですかね、、）
ポイント
「正の数を引くこと」は、
「負の数を足すこと」とおなじ
つまり、例題１の計算をくわしくみると、
というふうに考えることができます。
すみません、やはりまだ、
「正の数を引くこと」は、「負の数を足すこと」とおなじ
という考え方のイメージがつかめないです、、
では、すごろくの例をつかって、イメージしてみましょう！
例題１のイメージ｜すごろくの例
まず、すごろくの例では、現在地を、車のコマで表しています。
さらに、重要なポイントとして、
引き算は、車を後ろ方向へ下げる(バックする)ことだと考えることができます。
（一方で、たし算は、コマを前進させることでしたね。）
すごろくのイメージ｜ポイント
- 現在地を、車のコマであらわす
- ひき算は、車を後ろ方向へ下げる(バックする)こと
以上のポイントを頭にいれたうえで、
例題１を、すごろくの例でイメージすると、次のようになります。
コマの最初の位置は、+２
「ひき算される数」は、+２です。
+１マス分、後ろ方向に下がる
(バックする)
(バックする)
正の数である+１のひき算が行われます。
+１のマスに到着する
(+２)ー(+１)のひき算の結果、+１になりました。
今回の
\( (+2) – (+1) = +1 \)
という例題１のイメージはつかめました！
ただ、今回の例題１と、
「正負の数のたし算(加法)」の記事の例題３でやった
\( (+2) + (-1) = +1 \)
という数式は、本当に本質的には同じなんでしょうか？
すごろくのイメージでは、どちらも全然違うように見えるのですが、、
どちらの場合でも、やっていることは、本質的には同じです！
なぜなら、どちらのすごろくでも、
車の進む方向も、最後に到達するマス(答え)も同じだからです。
ただ、車に対する操作が真逆なので、
全然違うように見えてしまうわけです。
さらに具体的に説明していきましょう！
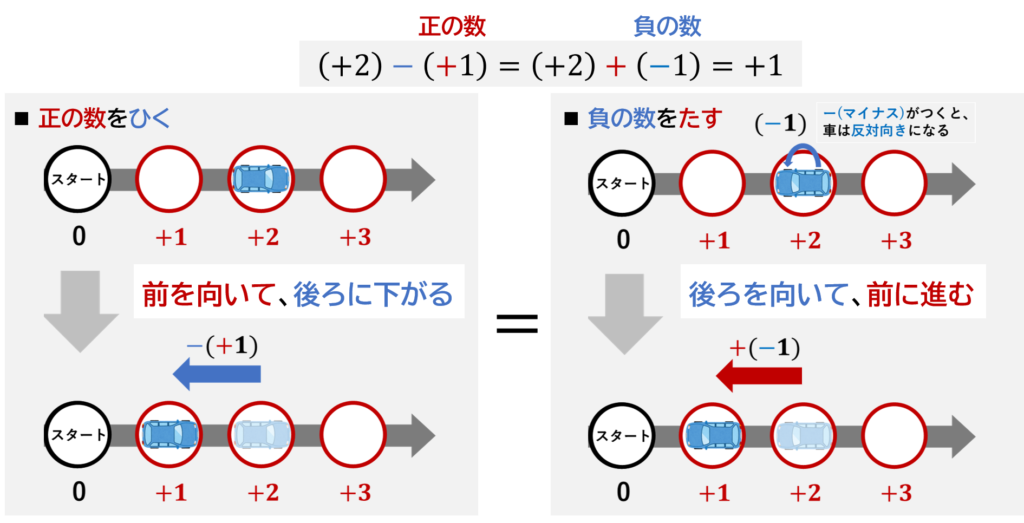
今回の例題１のすごろく例（正の数のひき算）では、
「車を前に向けて、後ろに下がる」ことで、
結果的に後ろ方向に進み、+１マスに到着しました。
一方、前回の「正負の数のたし算(加法)」の記事の例題３のすごろく例（負の数のたし算）では、
「車を後ろに向けて、前に進む」ことで、
結果的に後ろ方向に進み、+１マスに到着しました。
結局、どちらの場合も、同じ方向に進み、同じ場所に到着していますよね。
つまり、まとめると、
両者のすごろく上での違いは、
「車を前に向けて、後ろに下がる」か
「車を後ろに向けて、前に進む」か
の違いであり、
進む方向と到着する場所は同じ
ということになります。
実は、この違いは、冒頭で紹介したポイントである、
「正の数を引く」か、「負の数を足す」か
に対応していることもわかります。
この場合も、両者は本質的に同じでしたよね。
説明が長くなりましたが、要するに言いたいことは、
「正の数を引くこと」は、
「負の数を足すこと」とおなじ
だということです。
では、次に例題２をとおして、
「負の数をひく」とどうなるのかを見ていきましょう！
【例題２】負の数をひく
例題２
\( (+2) – (-1) = (+2) +1 = +3 \)
【例題２】負の数に、もう１つマイナス符号がつくと、正の数になる
「負の数をひく」という計算には、今回はじめて出会ったと思いますので、
「どう計算したらいいんだろう、、」と、少しこまりますよね。
でも計算のルールさえ分かってしまえば、悩むことなく簡単に計算できるようになります。
その計算のルールとは、
「負の数のひき算」の計算ルール
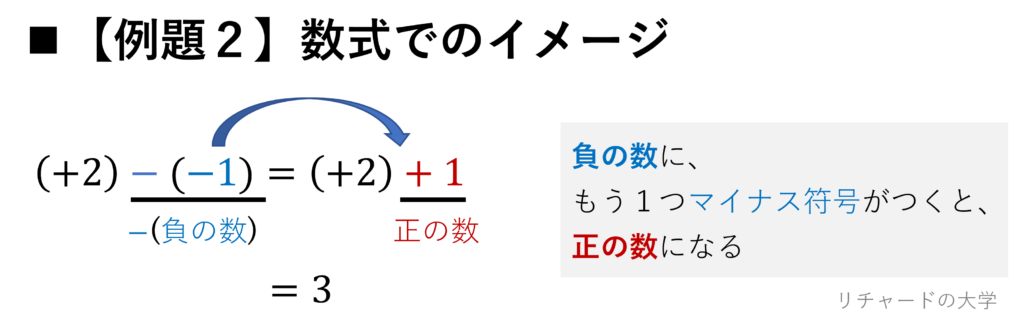
負の数に、もう１つー(マイナス符号)がつくと、正の数になる
例. \( – (-1) = +1 \)
というものです！
「負の数に、もう１つー(マイナス符号)がつくと、正の数になる」は、言い換えると、
「負の数をひくこと」は、
「正の数をたすこと」と同じである
とも言えます！
このルールを使うと、例題２は、次のように計算できます。
ちょっと待ってください！
どうして、「負の数をひくこと」が、「正の数をたすこと」と同じになるんですか？
ぜんぜん、イメージがわかないです、、
すみません、いきなり言われてもよくわからないですよね。
次の節で、すごろくのイメージを使って詳しく解説していきます！
例題２のイメージ｜すごろくの例
まず、すごろくの例では、現在地を、車のコマで表しています。
さらに、引き算は、車を後ろ方向へ下げる(バックする)ことだと考えることができます。
すごろくの例｜ポイント
- 現在地を、車のコマであらわす
- ひき算は、車を後ろ方向へ下げる(バックする)こと
さらに、正負の数１回目の記事で解説したように、
負の数は、正の数に対して、正反対の性質をもつため、
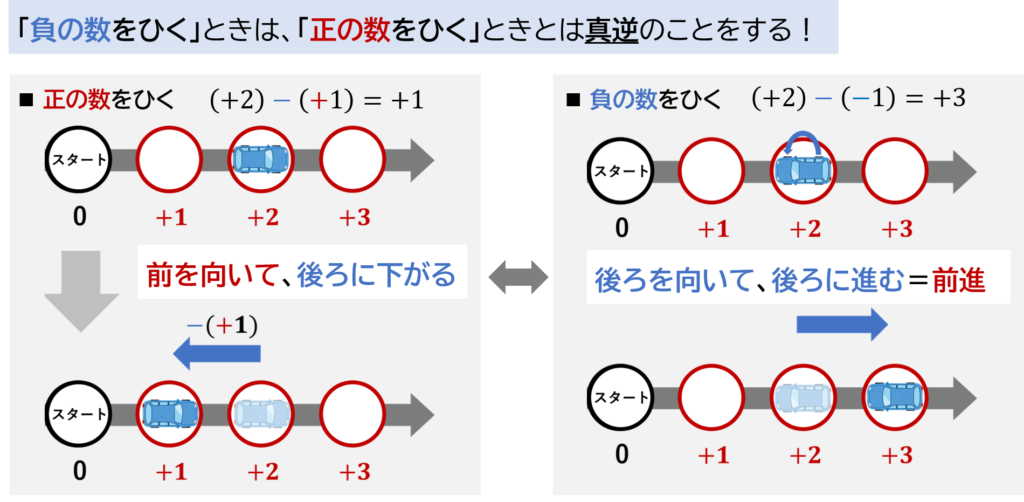
「負の数をひく」ときは、「正の数をひく」とき（後ろにバック）とは真逆のことをする
ことになります！
つまり、「負の数をひく」ときは、車のコマは、前進することになります！
以上のことをあたまに入れたうえで、次のすごろくのイメージをみてみましょう！
このイメージを使うと、例題２は次のステップで考えることができます！
コマの最初の位置は、+２
「たし算される数」は、+２です。
「引く数」が「負の数」であるため、
車を反対向きにする
車を反対向きにする
「負の数をひく」ときは、
「正の数をひく」ときと反対方向に、ひき算をすることになります。
車を反対向きにしたまま、
+１マスぶん、後ろにバックする
+１マスぶん、後ろにバックする
最初の位置(+２)に対して、
負の数ー(ー１)のひき算が行われます。
車を反対向きにしたまま、後ろにバックしているため、
結果として、車は、+１マス分、前方向に進みます
+３のマスに到着する
(+２)ー(ー１)のひき算の結果、+３になりました。
以上のステップをまとめると、次のようになります。
【例題２】すごろくを使ったイメージ
- スタートは（+２）であるため、
車はまず（+２）マスにいる - 「ひく数」にー（マイナス符号）が付いているため、
（「ひく数」が負の数であるため）
車を反対向きにする - 反対向きのまま、
車を（+１）マス後ろにバックする
(負の数(ー１)のひき算を行う） - 結果として、
車は+１マス前に進み、
+３マスに到達する
これが、すごろくの例をつかった、「負の数のひき算」のイメージです。
重要なことは、
「負の数をひく」ときには、
「正の数をひく」のときとは真逆のことをしている
ということです。
その結果、
「正の数をひく」場合では、
結果的に車は後ろ(マイナス方向)へ進み、
一方、
「負の数をひく」場合では、
結果的に車は前(プラス方向)へ進む
ことになります。
ここで、「正の数をたす」場合、車は前(プラス方向)へ進むことを思い出すと、
「負の数をひく」場合と、「正の数をたす」場合では、
どちらも前(プラス方向)へ進むという点で、結果は同じですよね。
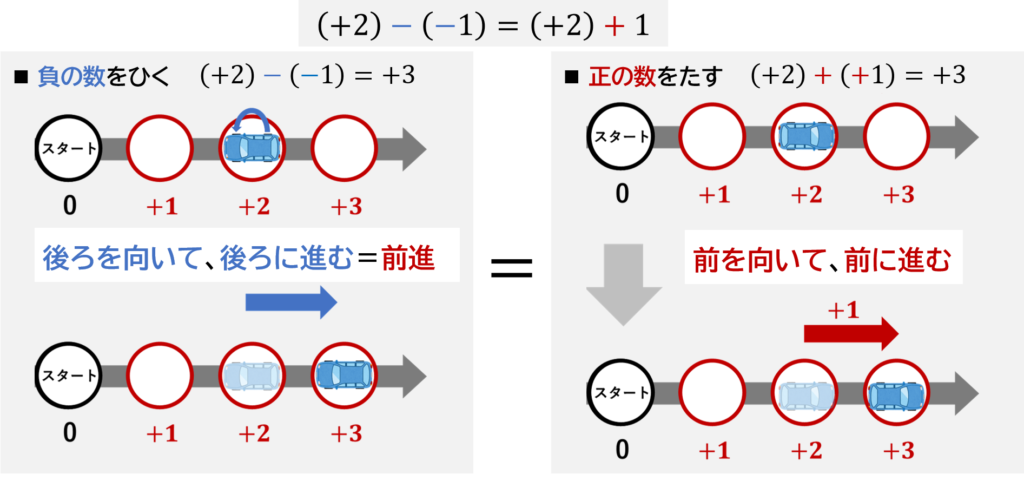
これが、冒頭でご説明したポイントの
「正の数をひくこと」は、
「負の数をたすこと」とおなじ
であることのイメージです。
この例をとおして、
「なぜ、負の数をひくと、正の数をたすことになるのか」のイメージを
なんとなくつかんでもらえたら嬉しいです！
まとめ｜すべての「ひき算」は、「たし算」とみなせる
例題１と例題２をとおして、
- 「正の数を引くこと」は、
「負の数を足すこと」とおなじ - 「負の数を引くこと」は、
「正の数を足すこと」とおなじ
ということを説明しました。
このことから、
どちらのひき算の場合でも、けっきょく、たし算とみなせることに気づくと思います。
冒頭でも述べたとおり、例題１と例題２が「正負の数のひき算」のパターンの全てです。
つまり、「正負の数のひき算」は、全て「正負の数のたし算」とみなせるということです。
ポイント
正負の数のひき算は、
すべて正負の数のたし算とみなせる
このポイントのメリットは、
そもそも「ひき算」というものを考えなくてよい点にあります。
なぜなら、このポイントを頭にいれると、
数式をみる度に「これってたし算だっけ？ひき算だっけ？」と悩まなくてすむからです。
これから、すべての「ひき算」が、「たし算」に見えるようになってくるくらい、
負の数のあつかいに慣れていきましょう！
それについては、次回の記事で解説していきますので、
お楽しみに！
次回の記事
「正負の数のかけ算(乗法)・わり算(除法)」の２つの計算ルールをわかりやすく解説！【要点のまとめ】【中１数学・正負の数④】
なお、この記事を書くにあたっては、以下の書籍も参考にしています。
created by Rinker
¥1,650
(2024/02/15 02:04:48時点 楽天市場調べ-詳細)
学校で習う順序とはまったく違うアプローチで、
「本質をおさえて、中学数学を最速で理解する」ことをコンセプトにした本であるため、
「あまり時間はないけど、中学数学の要点だけ抑えて、学び直したい！」
という学生や社会人の方に、非常におすすめです！
正直に言ってしまうと、このブログを見なくても、
この本さえ読めば、中学数学の本質は理解できます、、
ただ、「詳しさ」という点では、本ブログに分があると思うので、
必要に応じて、参考にしていただけると嬉しいです。
動画をつかった学習
また、ブログや書籍だけでなく、動画をつかった学習もオススメです！
その理由は、次の通りです！
動画での学習がオススメな理由
- 「目」と「耳」を使って学習ができるため、定着しやすいから
- 勉強のペースメーカーとなってくれるから
- 「ながら勉強」ができるから
動画をつかった学習の中でもオススメは、「スタディサプリ」です。
筆者も学生時代に使っていましたが、月額2,178円で利用できるため、
塾と比較すると、とても経済的です！
１４日間は無料で利用できるため、気になる方は試してみるといいかもしれません。↓
ABOUT ME
中学・高校では数学が苦手でしたが、
科学が好きだったため、
大学の物理学科に入るべく、数学を猛勉強。
その結果、なんとか物理学科に合格し、
そのまま大学院まで進学。
最終学歴は、物理学の修士号です。
数学が苦手だった経験をいかし、
私と同じように数学に苦しんでいる方の役に立てればと思い、
わかりやすさとイメージを重視して、
このブログを書いています。
科学が好きだったため、
大学の物理学科に入るべく、数学を猛勉強。
その結果、なんとか物理学科に合格し、
そのまま大学院まで進学。
最終学歴は、物理学の修士号です。
数学が苦手だった経験をいかし、
私と同じように数学に苦しんでいる方の役に立てればと思い、
わかりやすさとイメージを重視して、
このブログを書いています。
